Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Solution 4.4:7c

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (07:59, 14 October 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
If we want to solve the equation
+
If we want to solve the equation <math>\cos 3x = \sin 4x</math>, we need an additional result which tells us for which values of ''u'' and ''v'' the equality
-
<math>\text{cos 3}x=\text{sin 4}x</math>, we need an additional result which tells us for which values of
+
<math>\cos u = \sin v</math> holds, but to get that we have to start with the equality <math>\cos u=\cos v</math>.
-
<math>u</math>
+
-
and
+
-
<math>v</math>
+
-
the equality
+
-
<math>\text{cos }u=\text{sin }v</math>
+
-
holds, but to get that we have to start with the equality
+
-
<math>\cos u=\cos v</math>.
+
So, we start by looking at the equality
So, we start by looking at the equality
 +
{{Displayed math||<math>\cos u=\cos v\,\textrm{.}</math>}}
-
<math>\cos u=\cos v</math>
+
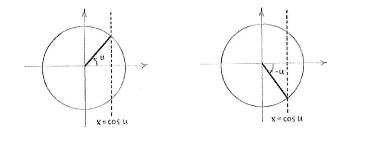
We know that for fixed ''u'' there are two angles <math>v=u</math> and <math>v=-u</math> in the unit circle which have the cosine value <math>\cos u</math>, i.e. their ''x''-coordinate is equal to <math>\cos u\,</math>.
-
 
+
-
 
+
-
We know that for fixed
+
-
<math>u</math>
+
-
there are two angles
+
-
<math>v=u\text{ }</math>
+
-
and
+
-
<math>v=-\text{u}</math>
+
-
in the unit circle which have the cosine value
+
-
<math>\cos u</math>, i.e. their
+
-
<math>x</math>
+
-
-coordinate is equal to
+
-
<math>\cos u</math>.
+
-
 
+
[[Image:4_4_7_c1.gif|center]]
[[Image:4_4_7_c1.gif|center]]
-
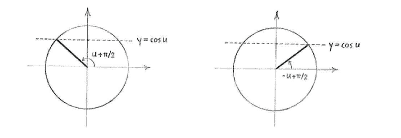
Imagine now that the whole unit circle is rotated anti-clockwise an angle
+
Imagine now that the whole unit circle is rotated anti-clockwise an angle <math>\pi/2</math>. The line <math>x=\cos u</math> will become the line <math>y=\cos u</math> and the angles ''u'' and -''u'' are rotated to <math>u+\pi/2</math> and <math>-u+\pi/2</math>, respectively.
-
<math>{\pi }/{2}\;</math>. The line
+
-
<math>x=\cos u</math>
+
-
will become the line
+
-
<math>y=\cos u</math>
+
-
and the angles
+
-
<math>u</math>
+
-
and
+
-
<math>-u</math>
+
-
are rotated to
+
-
<math>u+{\pi }/{2}\;</math>
+
-
and
+
-
<math>-u+{\pi }/{2}\;</math>, respectively.
+
-
 
+
[[Image:4_4_7_c2.gif|center]]
[[Image:4_4_7_c2.gif|center]]
-
The angles
+
The angles <math>u+\pi/2</math> and <math>-u+\pi/2</math> therefore have their ''y''-coordinate, and hence sine value, equal to <math>\cos u</math>. In other words, the equality
-
<math>u+{\pi }/{2}\;</math>
+
-
and
+
-
<math>-u+{\pi }/{2}\;</math>
+
-
therefore have their
+
-
<math>y</math>
+
-
-coordinate, and hence sine value, equal to
+
-
<math>\cos u</math>. In other words, the equality
+
-
 
+
-
 
+
-
<math>\text{cos }u=\text{sin }v</math>
+
-
 
+
-
 
+
-
holds for fixed
+
-
<math>u</math>
+
-
in the unit circle when
+
-
<math>v=\pm u+{\pi }/{2}\;</math>, and more generally when
+
-
 
+
-
<math>v=\pm u+\frac{\pi }{2}+2n\pi </math>
+
{{Displayed math||<math>\cos u = \sin v</math>}}
-
(
+
-
<math>n</math>
+
-
an arbitrary integer).
+
-
For our equation
+
holds for fixed ''u'' in the unit circle when <math>v = \pm u + \pi/2</math>, and more generally when
-
<math>\text{cos 3}x=\text{sin 4}x</math>, this result means that
+
-
<math>x\text{ }</math>
+
-
must satisfy
+
 +
{{Displayed math||<math>v = \pm u + \frac{\pi}{2} + 2n\pi\qquad</math>(''n'' is an arbitrary integer).}}
-
<math>4x=\pm 3x+\frac{\pi }{2}+2n\pi </math>
+
For our equation <math>\cos 3x = \sin 4x</math>, this result means that ''x'' must satisfy
 +
{{Displayed math||<math>4x = \pm 3x + \frac{\pi}{2} + 2n\pi\,\textrm{.}</math>}}
This means that the solutions to the equation are
This means that the solutions to the equation are
 +
{{Displayed math||<math>\left\{\begin{align}
 +
x &= \frac{\pi}{2} + 2n\pi\,,\\[5pt]
 +
x &= \frac{\pi}{14} + \frac{2}{7}\pi n\,,
 +
\end{align}\right.</math>}}
-
<math>\left\{ \begin{array}{*{35}l}
+
where ''n'' is an arbitrary integer.
-
x=\frac{\pi }{2}+2n\pi \\
+
-
x=\frac{\pi }{14}+\frac{2}{7}\pi n \\
+
-
\end{array} \right.</math>
+
-
(
+
-
<math>n</math>
+
-
an arbitrary integer)
+

Current revision

If we want to solve the equation cos3x=sin4x, we need an additional result which tells us for which values of u and v the equality cosu=sinv holds, but to get that we have to start with the equality cosu=cosv.

So, we start by looking at the equality

cosu=cosv.

We know that for fixed u there are two angles v=u and v=−u in the unit circle which have the cosine value cosu, i.e. their x-coordinate is equal to cosu.

Imagine now that the whole unit circle is rotated anti-clockwise an angle 2. The line x=cosu will become the line y=cosu and the angles u and -u are rotated to u+2 and −u+2, respectively.

The angles u+2 and −u+2 therefore have their y-coordinate, and hence sine value, equal to cosu. In other words, the equality

cosu=sinv

holds for fixed u in the unit circle when v=u+2, and more generally when

v=u+2+2n(n is an arbitrary integer).

For our equation cos3x=sin4x, this result means that x must satisfy

4x=3x+2+2n.

This means that the solutions to the equation are

xx=2+2n=14+72n

where n is an arbitrary integer.

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.4:7c"