Processing Math: Done
Solution 4.4:8a
From Förberedande kurs i matematik 1
(Difference between revisions)
m (Lösning 4.4:8a moved to Solution 4.4:8a: Robot: moved page) |
m |
||
| (One intermediate revision not shown.) | |||
| Line 1: | Line 1: | ||
| - | {{ | + | If we use the formula for double angles, <math>\sin 2x = 2\sin x\cos x</math>, and move all the terms over to the left-hand side, the equation becomes |
| - | < | + | |
| - | { | + | {{Displayed math||<math>2\sin x\cos x-\sqrt{2}\cos x=0\,\textrm{.}</math>}} |
| - | {{ | + | |
| - | < | + | Then, we see that we can take a factor <math>\cos x</math> out of both terms, |
| - | {{ | + | |
| + | {{Displayed math||<math>\cos x\,(2\sin x-\sqrt{2}) = 0</math>}} | ||
| + | |||
| + | and hence divide up the equation into two cases. The equation is satisfied either if <math>\cos x = 0</math> or if <math>2\sin x-\sqrt{2} = 0\,</math>. | ||
| + | |||
| + | |||
| + | <math>\cos x = 0</math>: | ||
| + | |||
| + | This equation has the general solution | ||
| + | |||
| + | {{Displayed math||<math>x = \frac{\pi}{2}+n\pi\qquad</math>(''n'' is an arbitrary integer).}} | ||
| + | |||
| + | |||
| + | <math>2\sin x-\sqrt{2}=0</math>: | ||
| + | |||
| + | If we collect <math>\sin x</math> on the left-hand side, we obtain the equation | ||
| + | <math>\sin x = 1/\!\sqrt{2}</math>, which has the general solution | ||
| + | |||
| + | {{Displayed math||<math>\left\{\begin{align} | ||
| + | x &= \frac{\pi}{4}+2n\pi\,,\\[5pt] | ||
| + | x &= \frac{3\pi}{4}+2n\pi\,, | ||
| + | \end{align}\right.</math>}} | ||
| + | |||
| + | where ''n'' is an arbitrary integer. | ||
| + | |||
| + | |||
| + | The complete solution of the equation is | ||
| + | |||
| + | {{Displayed math||<math>\left\{\begin{align} | ||
| + | x &= \frac{\pi}{4}+2n\pi\,,\\[5pt] | ||
| + | x &= \frac{\pi}{2}+n\pi\,,\\[5pt] | ||
| + | x &= \frac{3\pi}{4}+2n\pi\,, | ||
| + | \end{align}\right.</math>}} | ||
| + | |||
| + | where ''n'' is an arbitrary integer. | ||
Current revision
If we use the formula for double angles,
 2cosx=0. 2cosx=0. |
Then, we see that we can take a factor
 2)=0 2)=0 |
and hence divide up the equation into two cases. The equation is satisfied either if  2=0
2=0
This equation has the general solution
 2+n 2+n |
 2=0
2=0
If we collect 
 2
2
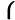 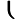 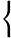   xx= xx= 4+2n 4+2n  =43 =43 +2n +2n  |
where n is an arbitrary integer.
The complete solution of the equation is
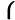             xxx= xxx= 4+2n 4+2n  = = 2+n 2+n  =43 =43 +2n +2n  |
where n is an arbitrary integer.
