4.1 Angles and circles

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m
Current revision (17:31, 10 November 2008) (edit) (undo)
 
(36 intermediate revisions not shown.)
Line 2: Line 2:
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
{| border="0" cellspacing="0" cellpadding="0" height="30" width="100%"
| style="border-bottom:1px solid #797979" width="5px" |  
| style="border-bottom:1px solid #797979" width="5px" |  
-
{{Mall:Vald flik|[[4.1 Vinklar och cirklar|Teori]]}}
+
{{Selected tab|[[4.1 Angles and circles|Theory]]}}
-
{{Mall:Ej vald flik|[[4.1 Övningar|Övningar]]}}
+
{{Not selected tab|[[4.1 Exercises|Exercises]]}}
| style="border-bottom:1px solid #797979" width="100%"|  
| style="border-bottom:1px solid #797979" width="100%"|  
|}
|}
{{Info|
{{Info|
-
'''Innehåll:'''
+
'''Contents:'''
-
*Olika vinkelmått (grader, radianer och varv)
+
*Various angle measures (degrees, radians and revolutions)
-
*Pythagoras sats
+
*The Pythagorean theorem
-
*Avståndsformeln i planet
+
*Formula for distance in the plane
-
*Cirkelns ekvation
+
* Equation of a circle
}}
}}
{{Info|
{{Info|
-
'''Lärandemål:'''
+
'''Learning outcomes:'''
-
Efter detta avsnitt ska du ha lärt dig att:
+
After this section, you will have learned :
-
*Omvandla mellan grader, radianer och varv.
+
*To convert between degrees, radians and revolutions.
-
*Beräkna arean och omkretsen av cirkelsektorer.
+
*To calculate the area and circumference of sectors of a circle.
-
*Känna till begreppen katet, hypotenusa och rätvinklig triangel.
+
*The features of right-angled triangles.
-
*Formulera och använda Pythagoras sats.
+
*To formulate and use the Pythagorean theorem.
-
*Beräkna avståndet mellan två punkter i planet.
+
*To calculate the distance between two points in the plane.
-
*Skissera cirklar med hjälp av att kvadratkomplettera deras ekvationer.
+
*To sketch circles by completing the square.
-
*Känna till begreppen enhetscirkel, tangent, radie, diameter, periferi, korda och cirkelbåge.
+
*The concepts of the unit circle, tangent, radius, diameter, circumference, chord and arc.
-
*Lösa geometriska problem som innehåller cirklar.
+
*To solve geometric problems that contain circles.
}}
}}
-
== Vinkelmått ==
+
== Angle measures ==
-
Det finns flera olika enheter för att mäta vinklar, som är praktiska i olika sammanhang. De två vanligaste vinkelmåtten i matematiken är grader och radianer.
+
There are several different units for measuring angles, which are used in different contexts. The two most common within mathematics are degrees and radians.
-
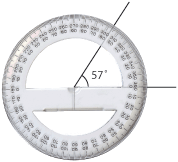
*'''Grader.''' Om ett helt varv delas in i 360 delar, så kallas varje del 1 grad. Beteckningen för grader är <math>{}^\circ</math>.
+
*'''Degrees.''' If a complete revolution is divided into 360 parts, then each part is called 1 degree. Degrees are designated by <math>{}^\circ</math>.
-
[[Bild:Gradskiva - 57°.gif||center]]
+
[[Image:Gradskiva - 57°.gif||center]]
-
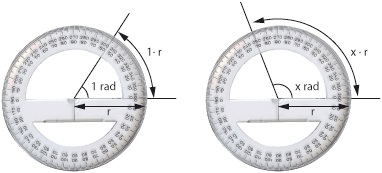
*'''Radianer.''' Ett annat sätt att mäta vinklar är att använda längden av vinkelns cirkelbåge i förhållande till radien som mått på vinkeln. Detta vinkelmått kallas för radian. Ett varv är alltså <math>2\pi</math> radianer eftersom cirkelns omkrets är <math>2\pi r</math>, där <math>r</math> är cirkelns radie.
+
*'''Radians.''' Another way to measure an angle, is to use the length of the arc described by the angle in relation to the radius. This unit is called radian. A revolution is <math>2\pi</math> radians, since the circumference of a circle is <math>2\pi r</math>, where <math>r</math> is the radius of the circle.
-
[[Bild:Gradskiva - Radianer.gif||center]]
+
[[Image:Gradskiva - Radianer.gif||center]]
-
Ett helt varv är <math>360^\circ</math> eller <math>2\pi</math> radianer och det gör att
+
A complete revolution is <math>360^\circ</math> or <math>2\pi</math> radians which means
-
{{Fristående formel||<math>\begin{align*}
+
{{Displayed math||<math>\begin{align*}
-
&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radianer }
+
&1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radians }
-
= \frac{\pi}{180}\ \mbox{ radianer,}\\
+
= \frac{\pi}{180}\ \mbox{ radians,}\\
&1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ
&1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ
= \frac{180^\circ}{\pi}\,\mbox{.}
= \frac{180^\circ}{\pi}\,\mbox{.}
\end{align*}</math>}}
\end{align*}</math>}}
-
Dessa omvandlingsfaktorer kan användas för att konvertera mellan grader och radianer.
+
These conversion relations can be used to convert between degrees and radians.
<div class="exempel">
<div class="exempel">
-
'''Exempel 1'''
+
''' Example 1'''
<ol type="a">
<ol type="a">
<li><math>30^\circ = 30 \cdot 1^\circ
<li><math>30^\circ = 30 \cdot 1^\circ
-
= 30 \cdot \frac{\pi}{180}\ \mbox{ radianer }
+
= 30 \cdot \frac{\pi}{180}\ \mbox{ radians }
-
= \frac{\pi}{6}\ \mbox{ radianer }</math></li>
+
= \frac{\pi}{6}\ \mbox{ radians }</math></li>
-
<li><math>\frac{\pi}{8}\ \mbox { radianer }
+
<li><math>\frac{\pi}{8}\ \mbox { radians }
= \frac{\pi}{8} \cdot (1 \; \mbox{radian}\,)
= \frac{\pi}{8} \cdot (1 \; \mbox{radian}\,)
= \frac{\pi}{8} \cdot \frac{180^\circ}{\pi}
= \frac{\pi}{8} \cdot \frac{180^\circ}{\pi}
-
= 22{,}5^\circ</math></li>
+
= 22\mbox{.}5^\circ</math></li>
</ol>
</ol>
</div>
</div>
-
I en del sammanhang kan det vara meningsfullt att tala om negativa vinklar eller vinklar som är större än 360°. Då kan man använda att man kan ange samma riktning med flera olika vinklar som skiljer sig från varandra med ett helt antal varv.
+
In some contexts, it may be useful to talk about negative angles and angles greater than 360°. This means that the same point on the circle can be designated by different angles that differ from each other by an integral number of revolutions.
-
<center>{{:4.1 - Figur - Vinklarna 45°, -315° och 405°}}</center>
+
<center>{{:4.1 - Figure - Angles 45°, -315° and 405°}}</center>
<div class="exempel">
<div class="exempel">
-
'''Exempel 2'''
+
''' Example 2'''
<ol type="a">
<ol type="a">
-
<li>Vinklarna <math>-55^\circ</math> och <math>665^\circ
+
<li> The angles <math>-55^\circ</math> and <math>665^\circ
-
</math> anger samma riktning eftersom
+
</math> indicate the same point on the circle because
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
-55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}</math>}}</li>
-55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}</math>}}</li>
-
<li>Vinklarna <math>\frac{3\pi}{7}</math> och <math>
+
<li> The angles <math>\frac{3\pi}{7}</math> and <math>
-
-\frac{11\pi}{7}</math> anger samma riktning eftersom
+
-\frac{11\pi}{7}</math> indicate the same point on the circle because
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
\frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}</math>}}</li>
\frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}</math>}}</li>
-
<li>Vinklarna <math>36^\circ</math> och <math>
+
<li> The angles <math>36^\circ</math> and <math>
-
216^\circ</math> anger inte samma riktning utan motsatta riktningar eftersom
+
216^\circ</math> do not specify the samepoint on the circle, but opposite points since
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
36^\circ + 180^\circ = 216^\circ\,\mbox{.}</math>}}</li>
36^\circ + 180^\circ = 216^\circ\,\mbox{.}</math>}}</li>
</ol>
</ol>
Line 92: Line 92:
-
== Avståndsformeln ==
+
== Formula for distance in the plane ==
-
Pythagoras sats är en av de mest kända satserna i matematiken och säger att i en rätvinklig triangel med kateter <math>a</math> och <math>b</math>, och hypotenusa <math>c</math> gäller att
+
The theorem of Pythagoras is one of the most famous theorems in mathematics and says that in a right-angled triangle with the legs <math>a</math> and <math>b</math>, and hypotenuse <math>c</math> then <math>a^2 + b^2 = c^2</math>.
<div class="regel">
<div class="regel">
{|width="100%"
{|width="100%"
-
|width="100%"|'''Pythagoras sats:'''
+
|width="100%"|'''The Pythagorean theorem:'''
-
{{Fristående formel||<math>c^2 = a^2 + b^2\,\mbox{.}</math>}}
+
{{Displayed math||<math>c^2 = a^2 + b^2\,\mbox{.}</math>}}
-
|align="right"|{{:4.1 - Figur - Pythagoras sats}}
+
|align="right"|{{:4.1 - Figure - The Pythagorean theorem}}
|}
|}
</div>
</div>
<div class="exempel">
<div class="exempel">
-
'''Exempel 3'''
+
''' Example 3'''
{| width="100%"
{| width="100%"
-
|width="100%"|I triangeln till höger är
+
|width="100%"| Consider the triangle on the right. Then
-
{{Fristående formel||<math>c^2= 3^2 + 4^2 = 9 +16 = 25</math>}}
+
{{Displayed math||<math>c^2= 3^2 + 4^2 = 9 +16 = 25</math>}}
-
och därför är hypotenusan <math>c</math> lika med
+
and therefore the hypotenuse <math>c</math> is equal to
-
{{Fristående formel||<math>c=\sqrt{25} = 5\,\mbox{.}</math>}}
+
{{Displayed math||<math>c=\sqrt{25} = 5\,\mbox{.}</math>}}
-
|align="right"|{{:4.1 - Figur - Rätvinklig triangel med sidor 3, 4 och 5}}
+
|align="right"|{{:4.1 - Figure - A right-angled triangle with sides 3, 4 and 5}}
|}
|}
</div>
</div>
-
Pythagoras sats kan användas för att beräkna avståndet mellan två punkter i ett koordinatsystem.
+
The Pythagorean theorem can be used to calculate the distance between two points in a coordinate system.
<div class="regel">
<div class="regel">
-
'''Avståndsformeln:'''
+
'''Formula for distance:'''
-
Avståndet <math>d</math> mellan två punkter med koordinater <math>(x,y)</math> och <math>(a,b)</math> är
+
The distance <math>d</math> between two points with coordinates <math>(x,y)</math> and <math>(a,b)</math> is
-
{{Fristående formel||<math>d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}</math>}}
+
{{Displayed math||<math>d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}</math>}}
</div>
</div>
-
Linjestycket mellan punkterna är hypotenusan i en rätvinklig triangel vars kateter är parallella med koordinataxlarna.
+
The line joining the points is the hypotenuse of a triangle whose legs are parallel to the coordinate axes.
-
<center>{{:4.1 - Figur - Avståndsformeln}}</center>
+
<center>{{:4.1 - Figure - The distance formula}}</center>
-
Kateternas längd är lika med beloppet av skillnaden i ''x''- och ''y''-led mellan punkterna, dvs. <math>|x-a|</math> respektive <math>|y-b|</math>. Pythagoras sats ger sedan avståndsformeln.
+
The legs of the triangle have lengths equal to the difference in the ''x''- and ''y''-directions of the points, that is <math>|x-a|</math> and <math>|y-b|</math>. The Pythagorean theorem then gives the formula for the distance.
<div class="exempel">
<div class="exempel">
-
'''Exempel 4'''
+
''' Example 4'''
<ol type="a">
<ol type="a">
-
<li>Avståndet mellan <math>(1,2)</math> och <math>(3,1)</math> är
+
<li>The distance between <math>(1,2)</math> and <math>(3,1)</math> is
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
d = \sqrt{ (1-3)^2 + (2-1)^2}
d = \sqrt{ (1-3)^2 + (2-1)^2}
= \sqrt{(-2)^2 + 1^2}
= \sqrt{(-2)^2 + 1^2}
Line 141: Line 141:
= \sqrt{5}\,\mbox{.}</math>}}</li>
= \sqrt{5}\,\mbox{.}</math>}}</li>
-
<li>Avståndet mellan <math>(-1,0)</math> och <math>(-2,-5)</math> är
+
<li>The distance between <math>(-1,0)</math> and <math>(-2,-5)</math> is
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2}
d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2}
= \sqrt{1^2 + 5^2}
= \sqrt{1^2 + 5^2}
Line 151: Line 151:
-
== Cirklar ==
+
== Circles ==
-
En cirkel består av alla punkter som befinner sig på ett visst fixt avstånd <math>r</math> från en punkt <math>(a,b)</math>.
+
A circle consists of all the points that are at a given fixed distance <math>r</math> from a point <math>(a,b)</math>.
-
<center>{{:4.1 - Figur - Cirkel}}</center>
+
<center>{{:4.1 - Figure - Circle}}</center>
-
Avståndet <math>r</math> kallas för cirkelns radie och punkten <math>(a,b)</math> för cirkelns medelpunkt. Figuren nedan visar andra viktiga cirkelbegrepp.
+
The distance <math>r</math> is called the circle's radius and the point <math>(a,b)</math> is its centre. The figure below shows the other important concepts.
{| align="center"
{| align="center"
-
|align="center" valign="bottom"|{{:4.1 - Figur - Diameter}}
+
|align="center" valign="bottom"|{{:4.1 - Figure - Diameter}}
|width="15px"|
|width="15px"|
-
|align="center" valign="bottom"|{{:4.1 - Figur - Tangent}}
+
|align="center" valign="bottom"|{{:4.1 - Figure - Tangent}}
|width="15px"|
|width="15px"|
-
|align="center" valign="bottom"|{{:4.1 - Figur - Korda}}
+
|align="center" valign="bottom"|{{:4.1 - Figure - The chord of a circle}}
|width="15px"|
|width="15px"|
-
|align="center" valign="bottom"|{{:4.1 - Figur - Sekant}}
+
|align="center" valign="bottom"|{{:4.1 - Figure - Secant}}
|-
|-
|align="center"|Diameter
|align="center"|Diameter
Line 173: Line 173:
|align="center"|Tangent
|align="center"|Tangent
||
||
-
|align="center"|Korda
+
|align="center"| Chord
||
||
-
|align="center"|Sekant
+
|align="center"| Secant
|-
|-
|height="15px"|
|height="15px"|
|-
|-
-
|align="center"|{{:4.1 - Figur - Cirkelbåge}}
+
|align="center"|{{:4.1 - Figure - Arc of a circle}}
||
||
-
|align="center"|{{:4.1 - Figur - Periferi}}
+
|align="center"|{{:4.1 - Figure - Circumference}}
||
||
-
|align="center"|{{:4.1 - Figur - Cirkelsektor}}
+
|align="center"|{{:4.1 - Figure - Sector of a circle}}
||
||
-
|align="center"|{{:4.1 - Figur - Cirkelsegment}}
+
|align="center"|{{:4.1 - Figure - Segment of a circle}}
|-
|-
-
|align="center"|Cirkelbåge
+
|align="center"| Arc of a circle
||
||
-
|align="center"|Periferi
+
|align="center"| Circumference
||
||
-
|align="center"|Cirkelsektor
+
|align="center"| Sector of a circle
||
||
-
|align="center"|Cirkelsegment
+
|align="center"|Segment of a circle
|}
|}
<div class="exempel">
<div class="exempel">
-
'''Exempel 5'''
+
''' Example 5'''
{| width="100%"
{| width="100%"
-
||En cirkelsektor är given i figuren till höger.
+
||A sector of a circle is shown in the figure on the right.
<ol type="a">
<ol type="a">
-
<li>Bestäm cirkelbågens längd.
+
<li> Determine its arc length .
<br>
<br>
<br>
<br>
-
Medelpunktsvinkeln <math>50^\circ</math> blir i radianer
+
The central angle is <math>50^\circ</math>. In radians this is
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
50^\circ = 50 \cdot 1^\circ
50^\circ = 50 \cdot 1^\circ
-
= 50 \cdot \frac{\pi}{180}\ \mbox{ radianer }
+
= 50 \cdot \frac{\pi}{180}\ \mbox{ radians }
-
= \frac{5\pi}{18}\ \mbox{ radianer. }</math>}}
+
= \frac{5\pi}{18}\ \mbox{ radians. }</math>}}
</li>
</li>
</ol>
</ol>
|align="right" valign="top"|
|align="right" valign="top"|
-
{{:4.1 - Figur - Cirkelsektor 50°}}
+
{{:4.1 - Figure - 50° sector of a circle}}
|}
|}
<ol style="list-style-type:none; padding-top:0; margin-top:0;">
<ol style="list-style-type:none; padding-top:0; margin-top:0;">
-
<li>På det sätt som radianer är definierat betyder detta att cirkelbågens längd är radien multiplicerat med vinkeln mätt i radianer,
+
<li>The way radians have been defined means that the arc length is the radius multiplied by the angle measured in radians, so that the arc length is
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
-
3 \cdot \frac{5\pi}{18}\ \mbox{ l.e. }
+
3 \cdot \frac{5\pi}{18}\ \mbox{units }
-
= \frac{5\pi}{6}\ \mbox{ l.e. }</math>}}</li>
+
= \frac{5\pi}{6}\ \mbox{ units . }</math>}}</li>
</ol>
</ol>
<ol type="a" start="2">
<ol type="a" start="2">
-
<li>Bestäm cirkelsektorns area.
+
<li>Determine the area of the circle segment.
<br>
<br>
<br>
<br>
-
Cirkelsektorns andel av hela cirkeln är
+
The segment's share of the entire circle is
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
\frac{50^\circ}{360^\circ} = \frac{5}{36}</math>}}
\frac{50^\circ}{360^\circ} = \frac{5}{36}</math>}}
-
och det betyder att dess area är <math>\frac{5}{36}</math> delar av cirkelns area som är <math>\pi r^2 = \pi 3^2 = 9\pi</math>, dvs.
+
and this means that its area is <math>\frac{5}{36}</math> parts of the circle area, which is <math>\pi r^2 = \pi 3^2 = 9\pi</math>. Hence the area is
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
-
\frac{5}{36} \cdot 9\pi\ \mbox{ a.e. }= \frac{5\pi}{4}\ \mbox{ a.e. }</math>}}</li>
+
\frac{5}{36} \cdot 9\pi\ \mbox{ units }= \frac{5\pi}{4}\ \mbox{ units. }</math>}}</li>
</ol>
</ol>
</div>
</div>
-
En punkt <math>(x,y)</math> ligger på cirkeln som har medelpunkt i <math>(a,b)</math> och radie <math>r</math> om dess avstånd till medelpunkten är lika med <math>r</math>. Detta villkor kan formuleras med avståndsformeln som
+
A point <math>(x,y)</math> lies on the circle that has its centre at <math>(a,b)</math> and radius <math>r</math>, if its distance from the centre is equal to <math>r</math>. This condition can be formulated with the distance formula.
<div class="regel">
<div class="regel">
{| width="100%"
{| width="100%"
-
||'''Cirkelns ekvation:'''
+
||'''Circle equation: '''
-
{{Fristående formel||<math>(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}</math>}}
+
{{Displayed math||<math>(x – a)^2 + (y – b)^2 = r^2\,\mbox{.}</math>}}
-
|align="right"|{{:4.1 - Figur - Cirkelns ekvation}}
+
|align="right"|{{:4.1 - Figure - Equation of a circle}}
|}
|}
</div>
</div>
<div class="exempel">
<div class="exempel">
-
'''Exempel 6'''
+
''' Example 6'''
{| width="100%"
{| width="100%"
|-
|-
|width="100%"|
|width="100%"|
<ol type="a">
<ol type="a">
-
<li><math>(x-1)^2 + (y-2)^2 = 9\quad</math> är ekvationen för en cirkel med medelpunkt i <math>(1,2)</math> och radie <math>\sqrt{9} = 3</math>.</li>
+
<li><math>(x-1)^2 + (y-2)^2 = 9\quad</math> is the equation for a circle with centre <math>(1,2)</math> and radius <math>\sqrt{9} = 3</math>.</li>
</ol>
</ol>
-
|align="right"|{{:4.1 - Figur - Ekvationen (x - 1)² + (y - 2)² = 9}}
+
|align="right"|{{:4.1 - Figure - The equation (x - 1)² + (y - 2)² = 9}}
|-
|-
|width="100%"|
|width="100%"|
<ol type="a" start=2>
<ol type="a" start=2>
-
<li><math>x^2 + (y-1)^2 = 1\quad</math> kan skrivas som <math>(x-0)^2 + (y-1)^2 = 1</math> och är ekvationen för en cirkel med medelpunkt i <math>(0,1)</math> och radie <math>\sqrt{1} = 1</math>.</li>
+
<li><math>x^2 + (y-1)^2 = 1\quad</math> can be written as <math>(x-0)^2 + (y-1)^2 = 1</math> and is the equation of a circle with centre <math>(0,1)</math> and radius <math>\sqrt{1} = 1</math>.</li>
</ol>
</ol>
-
|align="right"|{{:4.1 - Figur - Ekvationen x² + (y - 1)² = 1}}
+
|align="right"|{{:4.1 - Figure - The equation x² + (y - 1)² = 1}}
|-
|-
|width="100%"|
|width="100%"|
<ol type="a" start=3>
<ol type="a" start=3>
-
<li><math>(x+1)^2 + (y-3)^2 = 5\quad</math> kan skrivas som <math>(x-(-1))^2 + (y-3)^2 = 5</math> och är ekvationen för en cirkel med medelpunkt i <math>(-1,3)</math> och radie <math>\sqrt{5} \approx 2{,}236</math>.</li>
+
<li><math>(x+1)^2 + (y-3)^2 = 5\quad</math> can be written as <math>(x-(-1))^2 + (y-3)^2 = 5</math> and is the equation of a circle with centre <math>(-1,3)</math> and radius <math>\sqrt{5} \approx 2\textrm{.}236</math>.</li>
</ol>
</ol>
-
|align="right"|{{:4.1 - Figur - Ekvationen (x + 1)² + (y - 3)² = 5}}
+
|align="right"|{{:4.1 - Figure - The equation (x + 1)² + (y - 3)² = 5}}
|}
|}
</div>
</div>
<div class="exempel">
<div class="exempel">
-
'''Exempel 7'''
+
''' Example 7'''
<ol type="a">
<ol type="a">
-
<li>Ligger punkten <math>(1,2)</math> på cirkeln <math>(x-4)^2 +y^2=13</math>?
+
<li> Does the point <math>(1,2)</math> lie on the circle <math>(x-4)^2 +y^2=13</math>?
<br>
<br>
<br>
<br>
-
Stoppar vi in punktens koordinater <math>x=1</math> och <math>y=2</math> i cirkelns ekvation har vi att
+
Inserting the coordinates of the point <math>x=1</math> and <math>y=2</math> in the circle equation, we have that
-
{{Fristående formel||<math>\begin{align*}
+
{{Displayed math||<math>\begin{align*}
-
\mbox{VL } &= (1-4)^2+2^2\\
+
\mbox{LHS } &= (1-4)^2+2^2\\
-
&= (-3)^2+2^2 = 9+4 = 13 = \mbox{HL}\,\mbox{.}
+
&= (-3)^2+2^2 = 9+4 = 13 = \mbox{RHS}\,\mbox{.}
\end{align*}</math>}}
\end{align*}</math>}}
-
Eftersom punkten uppfyller cirkelns ekvation ligger punken på cirkeln.
+
Since the point satisfies the circle equation it lies on the circle.
-
<center>{{:4.1 - Figur - Ekvationen (x - 4)² + y² = 13}}</center></li>
+
<center>{{:4.1 - Figure - The equation (x - 4)² + y² = 13}}</center></li>
-
<li>Bestäm ekvationen för cirkeln som har medelpunkt i <math>(3,4)</math> och innehåller punkten <math>(1,0)</math>.
+
<li> Determine the equation for the circle that has its centre at <math>(3,4)</math> and goes through the point <math>(1,0)</math>.
<br>
<br>
<br>
<br>
-
Eftersom punkten <math>(1,0)</math> ska ligga på cirkeln måste cirkelns radie vara lika med avståndet från <math>(1,0)</math> till medelpunkten <math>(3,4)</math>. Avståndsformeln ger att detta avstånd är
+
Since the point <math>(1,0)</math> lies on the circle, the radius of the circle must be equal to the distance of the point from <math>(1,0)</math> to the centre <math>(3,4)</math>. The distance formula allows us to calculate that this distance is
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{.}</math>}}
c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{.}</math>}}
-
Cirkelns ekvation är därför
+
The circle equation is therefore
-
{{Fristående formel||<math>(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}</math>}}
+
{{Displayed math||<math>(x-3)^2 + (y-4)^2 = 20 \; \mbox{.}</math>}}
-
<center>{{:4.1 - Figur - Ekvationen (x - 3)² + (y - 4)² = 20}}</center></li>
+
<center>{{:4.1 - Figure - The equation (x - 3)² + (y - 4)² = 20}}</center></li>
</ol>
</ol>
</div>
</div>
Line 296: Line 296:
<div class="exempel">
<div class="exempel">
-
'''Exempel 8'''
+
''' Example 8'''
-
Bestäm medelpunkt och radie för den cirkel vars ekvation är <math>\ x^2 + y^2 – 2x + 4y + 1 = 0</math>.
+
Determine the centre and radius of the circle with equation <math>\ x^2 + y^2 – 2x + 4y + 1 = 0</math>.
-
Vi ska försöka skriva om cirkelns ekvation på formen
+
Let us try to write the equation in the form
-
{{Fristående formel||<math>(x – a)^2 + (y – b)^2 = r^2</math>}}
+
{{Displayed math||<math>(x – a)^2 + (y – b)^2 = r^2</math>}}
-
för då kan vi direkt avläsa att medelpunken är <math>(a,b)</math> och radien är <math>r</math>.
+
because then we can directly read from this that the centre is <math>(a,b)</math> and the radius is <math>r</math>.
-
Börja med att kvadratkomplettera termerna som innehåller <math>x</math> i vänsterledet
+
Start by completing the square for the terms containing <math>x</math> on the left-hand side
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
\underline{x^2-2x\vphantom{(}} + y^2+4y + 1
\underline{x^2-2x\vphantom{(}} + y^2+4y + 1
= \underline{(x-1)^2-1^2} + y^2+4y + 1</math>}}
= \underline{(x-1)^2-1^2} + y^2+4y + 1</math>}}
-
(de understrukna termerna visar kvadratkompletteringen).
+
The underlined terms shows the terms involved.
-
Kvadratkomplettera sedan termerna som innehåller <math>y</math>
+
Now complete the square for the terms containing <math>y</math>
-
{{Fristående formel||<math>
+
{{Displayed math||<math>
(x-1)^2-1^2 + \underline{y^2+4y} + 1
(x-1)^2-1^2 + \underline{y^2+4y} + 1
= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}</math>}}
= (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}</math>}}
-
Vänsterledet är alltså lika med
+
The left-hand side is therefore equal to
-
{{Fristående formel||<math> (x-1)^2 + (y+2)^2-4 </math>}}
+
{{Displayed math||<math> (x-1)^2 + (y+2)^2-4 </math>.}}
-
och flyttar vi över 4 till högerledet är cirkelns ekvation
+
Rearranging we see that the original equation is equivalent to
-
{{Fristående formel||<math> (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}</math>}}
+
{{Displayed math||<math> (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}</math>}}
-
Vi avläser att medelpunkten är <math>(1,-2)</math> och radien är <math>\sqrt{4}= 2</math>.
+
From this we can easily see that the centre is <math>(1,-2)</math> and the radius is <math>\sqrt{4}= 2</math>.
-
<center>{{:4.1 - Figur - Ekvationen x² + y² - 2x + 4y + 1 = 0}}</center>
+
<center>{{:4.1 - Figure - The equation x² + y² - 2x + 4y + 1 = 0}}</center>
</div>
</div>
-
[[4.1 Övningar|Övningar]]
+
[[4.1 Exercises|Exercises]]
<div class="inforuta" style="width:580px;">
<div class="inforuta" style="width:580px;">
-
'''Råd för inläsning'''
+
'''Study advice'''
-
'''Grund- och slutprov'''
+
'''The basic and final tests'''
-
Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge.
+
After you have read the text and worked through the exercises, you should do the basic and final tests to pass this section. You can find the link to the tests in your student lounge.
-
'''Tänk på att:'''
+
'''Keep in mind that...'''
-
'''Lästips'''
+
'''Reviews'''
-
för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om:
+
For those of you who want to deepen your understanding or need more detailed explanations consider the following references:
-
[http://sv.wikipedia.org/wiki/Pythagoras_sats Läs mer om Pythagoras sats på svenska Wikipedia]
+
[http://sv.wikipedia.org/wiki/Pythagoras_sats Learn more about Pythagoras theorem from Wikipedia ]
-
[http://mathworld.wolfram.com/Circle.html Läs mer i Mathworld om cirkeln]
+
[http://mathworld.wolfram.com/Circle.html Read more about the circle on the Mathworld website]
-
'''Länktips'''
+
'''Useful web sites'''
-
[http://www.math.kth.se/online/images/sinus_och_cosinus_i_enhetscirkeln.swf Interaktivt experiment: sinus och cosinus i enhetscirkeln] (Flash)
+
[http://www.math.kth.se/online/images/sinus_och_cosinus_i_enhetscirkeln.swf Interactive experiments: the sine and cosine on the unit circle ] (Flash)
</div>
</div>

Current revision

       Theory          Exercises      

Contents:

  • Various angle measures (degrees, radians and revolutions)
  • The Pythagorean theorem
  • Formula for distance in the plane
  • Equation of a circle

Learning outcomes:

After this section, you will have learned :

  • To convert between degrees, radians and revolutions.
  • To calculate the area and circumference of sectors of a circle.
  • The features of right-angled triangles.
  • To formulate and use the Pythagorean theorem.
  • To calculate the distance between two points in the plane.
  • To sketch circles by completing the square.
  • The concepts of the unit circle, tangent, radius, diameter, circumference, chord and arc.
  • To solve geometric problems that contain circles.

Angle measures

There are several different units for measuring angles, which are used in different contexts. The two most common within mathematics are degrees and radians.

  • Degrees. If a complete revolution is divided into 360 parts, then each part is called 1 degree. Degrees are designated by \displaystyle {}^\circ.
  • Radians. Another way to measure an angle, is to use the length of the arc described by the angle in relation to the radius. This unit is called radian. A revolution is \displaystyle 2\pi radians, since the circumference of a circle is \displaystyle 2\pi r, where \displaystyle r is the radius of the circle.


A complete revolution is \displaystyle 360^\circ or \displaystyle 2\pi radians which means

\displaystyle \begin{align*} 
   &1^\circ = \frac{1}{360} \cdot 2\pi\ \mbox{ radians }
            = \frac{\pi}{180}\ \mbox{ radians,}\\
   &1\ \mbox{ radian } = \frac{1}{2\pi} \cdot 360^\circ
            = \frac{180^\circ}{\pi}\,\mbox{.}
 \end{align*}

These conversion relations can be used to convert between degrees and radians.

Example 1

  1. \displaystyle 30^\circ = 30 \cdot 1^\circ = 30 \cdot \frac{\pi}{180}\ \mbox{ radians } = \frac{\pi}{6}\ \mbox{ radians }
  2. \displaystyle \frac{\pi}{8}\ \mbox { radians } = \frac{\pi}{8} \cdot (1 \; \mbox{radian}\,) = \frac{\pi}{8} \cdot \frac{180^\circ}{\pi} = 22\mbox{.}5^\circ

In some contexts, it may be useful to talk about negative angles and angles greater than 360°. This means that the same point on the circle can be designated by different angles that differ from each other by an integral number of revolutions.

[Image]

Example 2

  1. The angles \displaystyle -55^\circ and \displaystyle 665^\circ indicate the same point on the circle because
    \displaystyle 
     -55^\circ + 2 \cdot 360^\circ = 665^\circ\,\mbox{.}
  2. The angles \displaystyle \frac{3\pi}{7} and \displaystyle -\frac{11\pi}{7} indicate the same point on the circle because
    \displaystyle 
     \frac{3\pi}{7} - 2\pi = -\frac{11\pi}{7}\,\mbox{.}
  3. The angles \displaystyle 36^\circ and \displaystyle 216^\circ do not specify the samepoint on the circle, but opposite points since
    \displaystyle 
     36^\circ + 180^\circ = 216^\circ\,\mbox{.}


Formula for distance in the plane

The theorem of Pythagoras is one of the most famous theorems in mathematics and says that in a right-angled triangle with the legs \displaystyle a and \displaystyle b, and hypotenuse \displaystyle c then \displaystyle a^2 + b^2 = c^2.

The Pythagorean theorem:
\displaystyle c^2 = a^2 + b^2\,\mbox{.}

[Image]

Example 3

Consider the triangle on the right. Then
\displaystyle c^2= 3^2 + 4^2 = 9 +16 = 25

and therefore the hypotenuse \displaystyle c is equal to

\displaystyle c=\sqrt{25} = 5\,\mbox{.}

[Image]

The Pythagorean theorem can be used to calculate the distance between two points in a coordinate system.

Formula for distance:

The distance \displaystyle d between two points with coordinates \displaystyle (x,y) and \displaystyle (a,b) is

\displaystyle d = \sqrt{(x – a)^2 + (y – b)^2}\,\mbox{.}

The line joining the points is the hypotenuse of a triangle whose legs are parallel to the coordinate axes.

[Image]

The legs of the triangle have lengths equal to the difference in the x- and y-directions of the points, that is \displaystyle |x-a| and \displaystyle |y-b|. The Pythagorean theorem then gives the formula for the distance.

Example 4

  1. The distance between \displaystyle (1,2) and \displaystyle (3,1) is
    \displaystyle 
     d = \sqrt{ (1-3)^2 + (2-1)^2}
   = \sqrt{(-2)^2 + 1^2}
   = \sqrt{ 4+1}
   = \sqrt{5}\,\mbox{.}
  2. The distance between \displaystyle (-1,0) and \displaystyle (-2,-5) is
    \displaystyle 
     d = \sqrt{ (-1-(-2))^2 + (0-(-5))^2}
   = \sqrt{1^2 + 5^2}
   = \sqrt{1+25}
   = \sqrt{26}\,\mbox{.}


Circles

A circle consists of all the points that are at a given fixed distance \displaystyle r from a point \displaystyle (a,b).

[Image]


The distance \displaystyle r is called the circle's radius and the point \displaystyle (a,b) is its centre. The figure below shows the other important concepts.

[Image]

[Image]

[Image]

[Image]

Diameter Tangent Chord Secant

[Image]

[Image]

[Image]

[Image]

Arc of a circle Circumference Sector of a circle Segment of a circle

Example 5

A sector of a circle is shown in the figure on the right.
  1. Determine its arc length .

    The central angle is \displaystyle 50^\circ. In radians this is
    \displaystyle 
     50^\circ = 50 \cdot 1^\circ
          = 50 \cdot \frac{\pi}{180}\ \mbox{ radians }
          = \frac{5\pi}{18}\ \mbox{ radians. }

[Image]

  1. The way radians have been defined means that the arc length is the radius multiplied by the angle measured in radians, so that the arc length is
    \displaystyle 
     3 \cdot \frac{5\pi}{18}\ \mbox{units }
 = \frac{5\pi}{6}\ \mbox{ units . }
  1. Determine the area of the circle segment.

    The segment's share of the entire circle is
    \displaystyle 
     \frac{50^\circ}{360^\circ} = \frac{5}{36}

    and this means that its area is \displaystyle \frac{5}{36} parts of the circle area, which is \displaystyle \pi r^2 = \pi 3^2 = 9\pi. Hence the area is

    \displaystyle 
     \frac{5}{36} \cdot 9\pi\ \mbox{ units }= \frac{5\pi}{4}\ \mbox{ units. }

A point \displaystyle (x,y) lies on the circle that has its centre at \displaystyle (a,b) and radius \displaystyle r, if its distance from the centre is equal to \displaystyle r. This condition can be formulated with the distance formula.

Circle equation:
\displaystyle (x – a)^2 + (y – b)^2 = r^2\,\mbox{.}

[Image]

Example 6

  1. \displaystyle (x-1)^2 + (y-2)^2 = 9\quad is the equation for a circle with centre \displaystyle (1,2) and radius \displaystyle \sqrt{9} = 3.

[Image]

  1. \displaystyle x^2 + (y-1)^2 = 1\quad can be written as \displaystyle (x-0)^2 + (y-1)^2 = 1 and is the equation of a circle with centre \displaystyle (0,1) and radius \displaystyle \sqrt{1} = 1.

[Image]

  1. \displaystyle (x+1)^2 + (y-3)^2 = 5\quad can be written as \displaystyle (x-(-1))^2 + (y-3)^2 = 5 and is the equation of a circle with centre \displaystyle (-1,3) and radius \displaystyle \sqrt{5} \approx 2\textrm{.}236.

[Image]

Example 7

  1. Does the point \displaystyle (1,2) lie on the circle \displaystyle (x-4)^2 +y^2=13?

    Inserting the coordinates of the point \displaystyle x=1 and \displaystyle y=2 in the circle equation, we have that
    \displaystyle \begin{align*} 
       \mbox{LHS } &= (1-4)^2+2^2\\
              &= (-3)^2+2^2 = 9+4 = 13 = \mbox{RHS}\,\mbox{.}
 \end{align*}

    Since the point satisfies the circle equation it lies on the circle.

    [Image]

  2. Determine the equation for the circle that has its centre at \displaystyle (3,4) and goes through the point \displaystyle (1,0).

    Since the point \displaystyle (1,0) lies on the circle, the radius of the circle must be equal to the distance of the point from \displaystyle (1,0) to the centre \displaystyle (3,4). The distance formula allows us to calculate that this distance is
    \displaystyle 
     c = \sqrt{(3-1)^2 + (4-0)^2} = \sqrt{4 +16} = \sqrt{20} \, \mbox{.}

    The circle equation is therefore

    \displaystyle (x-3)^2 + (y-4)^2 = 20 \; \mbox{.}

    [Image]


Example 8

Determine the centre and radius of the circle with equation \displaystyle \ x^2 + y^2 – 2x + 4y + 1 = 0.


Let us try to write the equation in the form

\displaystyle (x – a)^2 + (y – b)^2 = r^2

because then we can directly read from this that the centre is \displaystyle (a,b) and the radius is \displaystyle r.

Start by completing the square for the terms containing \displaystyle x on the left-hand side

\displaystyle 
 \underline{x^2-2x\vphantom{(}} + y^2+4y + 1
 = \underline{(x-1)^2-1^2} + y^2+4y + 1

The underlined terms shows the terms involved.

Now complete the square for the terms containing \displaystyle y

\displaystyle 
 (x-1)^2-1^2 + \underline{y^2+4y} + 1
 = (x-1)^2-1^2 + \underline{(y+2)^2-2^2} + 1\,\mbox{.}

The left-hand side is therefore equal to

\displaystyle (x-1)^2 + (y+2)^2-4 .

Rearranging we see that the original equation is equivalent to

\displaystyle (x-1)^2 + (y+2)^2 = 4 \, \mbox{.}

From this we can easily see that the centre is \displaystyle (1,-2) and the radius is \displaystyle \sqrt{4}= 2.

[Image]


Exercises

Study advice

The basic and final tests

After you have read the text and worked through the exercises, you should do the basic and final tests to pass this section. You can find the link to the tests in your student lounge.


Keep in mind that...


Reviews

For those of you who want to deepen your understanding or need more detailed explanations consider the following references:

Learn more about Pythagoras theorem from Wikipedia

Read more about the circle on the Mathworld website


Useful web sites

Interactive experiments: the sine and cosine on the unit circle (Flash)

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/4.1_Angles_and_circles"