Processing Math: Done
Solution 4.2:1b
From Förberedande kurs i matematik 1
(Difference between revisions)
m (Lösning 4.2:1b moved to Solution 4.2:1b: Robot: moved page) |
m |
||
| (One intermediate revision not shown.) | |||
| Line 1: | Line 1: | ||
| - | + | If we reflect the triangle, it can be easier to identify the different sides in the triangle. | |
| - | + | ||
| - | + | ||
[[Image:4_2_1_b.gif|center]] | [[Image:4_2_1_b.gif|center]] | ||
| + | |||
| + | Because we know the hypotenuse and want to find the adjacent, it is appropriate to consider to the quotient for the cosine of an angle, | ||
| + | |||
| + | {{Displayed math||<math>\cos 32 = \frac{x}{25}\quad \Bigl({}=\frac{\text{adjacent}}{\text{hypotenuse }}\Bigr)\,\textrm{.}</math>}} | ||
| + | |||
| + | From this equation, we can solve for ''x'', | ||
| + | |||
| + | {{Displayed math||<math>x = 25\cdot \cos 32\quad ({}\approx 21\textrm{.}2)\,\textrm{.}</math>}} | ||
Current revision
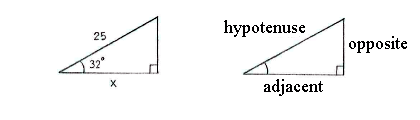
If we reflect the triangle, it can be easier to identify the different sides in the triangle.
Because we know the hypotenuse and want to find the adjacent, it is appropriate to consider to the quotient for the cosine of an angle,
 =adjacenthypotenuse  . |
From this equation, we can solve for x,
 cos32( 21.2). |
