Solution 2.1:7c
From Förberedande kurs i matematik 1
(Difference between revisions)
(Ny sida: {{NAVCONTENT_START}} <center> Bild:2_1_7c.gif </center> {{NAVCONTENT_STOP}}) |
m |
||
| (3 intermediate revisions not shown.) | |||
| Line 1: | Line 1: | ||
| - | {{ | + | We multiply the top and bottom of the first term by <math>a+1</math>, so that both terms then have the same denominator, |
| - | < | + | |
| - | {{ | + | {{Displayed math||<math>\frac{ax}{a+1}\cdot\frac{a+1}{a+1} - \frac{ax^{2}}{(a+1)^{2}} = \frac{ax(a+1)-ax^{2}}{(a+1)^{2}}\,\textrm{.}</math>}} |
| + | |||
| + | Because both terms in the numerator contain the factor <math>ax</math>, we take out that factor, obtaining | ||
| + | |||
| + | {{Displayed math||<math>\frac{ax(a+1-x)}{(a+1)^{2}}</math>}} | ||
| + | |||
| + | and see that the answer cannot be simplified any further. | ||
| + | |||
| + | Note: It is only factors in the numerator and denominator that can cancel each other out, not individual terms. Hence, the following "cancellation" is wrong | ||
| + | |||
| + | {{Displayed math||<math>\frac{ax(\rlap{/\,/\,/\,/}a+1)-ax^2}{(a+1)^{2\llap{/}}} = \frac{ax-ax^{2}}{a+1}\,\textrm{.}</math>}} | ||
Current revision
We multiply the top and bottom of the first term by
 a+1a+1−ax2(a+1)2=(a+1)2ax(a+1)−ax2. a+1a+1−ax2(a+1)2=(a+1)2ax(a+1)−ax2. |
Because both terms in the numerator contain the factor
and see that the answer cannot be simplified any further.
Note: It is only factors in the numerator and denominator that can cancel each other out, not individual terms. Hence, the following "cancellation" is wrong
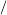 ax( ax(    a+1)−ax2=a+1ax−ax2. a+1)−ax2=a+1ax−ax2. |
