Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Solution 2.3:8b

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m
Line 1: Line 1:
-
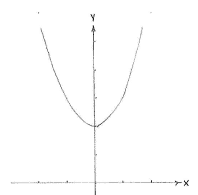
As a starting point, we can take the curve
+
As a starting point, we can take the curve <math>y=x^{2}+2</math> which is a parabola with a minimum at (0,2) and is sketched further down. Compared with that curve,
-
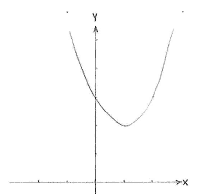
<math>y=x^{2}+2</math>
+
<math>y = (x-1)^{2}+2</math> is the same curve in which we must consistently choose ''x'' to be one unit greater in order to get the same ''y''-value. The curve <math>y = (x-1)^{2}+2</math> is thus shifted one unit to the right compared with <math>y=x^{2}+2</math>.
-
which is a parabola with a minimum at
+
-
<math>\left( 0 \right.,\left. 2 \right)</math>
+
-
and is sketched further down. Compared with that curve,
+
-
<math>y=\left( x-1 \right)^{2}+2</math>
+
-
is the same curve in which we must consistently choose
+
-
<math>x</math>
+
-
to be one unit greater in order to get the same
+
-
<math>y</math>
+
-
-value. The curve
+
-
<math>y=\left( x-1 \right)^{2}+2</math>
+
-
is thus shifted one unit to the right compared with
+
-
<math>y=x^{2}+2</math>.
+
-
[[Image:2_3_8_b.gif|center]]
+
{| align="center"
 +
||[[Image:2_3_8_b-1.gif|center]]
 +
|width="10px"|&nbsp;
 +
||[[Image:2_3_8_b-2.gif|center]]
 +
|-
 +
||<small>The graph of ''f''(''x'')&nbsp;=&nbsp;''x''²&nbsp;+&nbsp;2</small>
 +
||
 +
||<small>The graph of ''f''(''x'')&nbsp;=&nbsp;(''x''&nbsp;-&nbsp;1)²&nbsp;+&nbsp;2</small>
 +
|}

Revision as of 12:56, 29 September 2008

As a starting point, we can take the curve y=x2+2 which is a parabola with a minimum at (0,2) and is sketched further down. Compared with that curve, y=(x−1)2+2 is the same curve in which we must consistently choose x to be one unit greater in order to get the same y-value. The curve y=(x−1)2+2 is thus shifted one unit to the right compared with y=x2+2.


 
The graph of f(x) = x² + 2 The graph of f(x) = (x - 1)² + 2
Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_2.3:8b"