Solution 2.2:9a
From Förberedande kurs i matematik 1
m (Lösning 2.2:9a moved to Solution 2.2:9a: Robot: moved page) |
|||
| Line 1: | Line 1: | ||
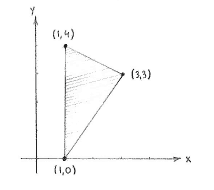
| + | We can start by drawing the points | ||
| + | <math>\left( 1 \right.,\left. 4 \right)</math>, | ||
| + | <math>\left( 3 \right.,\left. 3 \right)</math> | ||
| + | and | ||
| + | <math>\left( 1 \right.,\left. 0 \right)</math> | ||
| + | in a coordinate system and draw lines between them, so that we get a picture of how thetriangle looks. | ||
| + | |||
{{NAVCONTENT_START}} | {{NAVCONTENT_START}} | ||
[[Image:2_2_9_a-1(2).gif|center]] | [[Image:2_2_9_a-1(2).gif|center]] | ||
| - | + | ||
{{NAVCONTENT_STOP}} | {{NAVCONTENT_STOP}} | ||
| + | |||
| + | If we now think of how we should use the fact that the area of a triangle is given by the formula | ||
| + | |||
| + | Area= | ||
| + | <math>\frac{1}{2}</math> | ||
| + | (base)∙(height), | ||
| + | |||
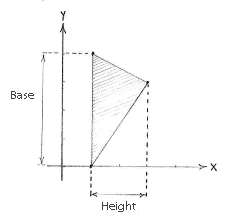
| + | it is clear that it is most appropriate to use the edge from | ||
| + | <math>\left( 1 \right.,\left. 0 \right)</math> | ||
| + | to | ||
| + | <math>\left( 1 \right.,\left. 4 \right)</math> | ||
| + | as the base of the triangle. | ||
| + | The base is then parallel with the y-axis and we can read off its length as the difference in the | ||
| + | |||
| + | <math>y</math> | ||
| + | -coordinate between the corner points | ||
| + | <math>\left( 1 \right.,\left. 0 \right)</math> | ||
| + | and | ||
| + | <math>\left( 1 \right.,\left. 4 \right)</math>, i.e. | ||
| + | |||
| + | base | ||
| + | <math>=4-0=0</math>. | ||
| + | In addition, the triangle's height is the horizontal distance from the third corner point | ||
| + | <math>\left( 3 \right.,\left. 3 \right)</math> | ||
| + | to the base and we can read that off as the difference in the | ||
| + | <math>x</math> | ||
| + | -direction between | ||
| + | <math>\left( 3 \right.,\left. 3 \right)</math> | ||
| + | and the line | ||
| + | <math>x=1</math>, i.e. | ||
| + | |||
| + | height | ||
| + | <math>=3-1=2</math>. | ||
| + | |||
{{NAVCONTENT_START}} | {{NAVCONTENT_START}} | ||
[[Image:2_2_9_a-2(2).gif|center]] | [[Image:2_2_9_a-2(2).gif|center]] | ||
| - | + | ||
{{NAVCONTENT_STOP}} | {{NAVCONTENT_STOP}} | ||
| + | |||
| + | Thus, the triangle's area is | ||
| + | |||
| + | Area= | ||
| + | <math>\frac{1}{2}</math> | ||
| + | (base)∙(height) | ||
| + | <math>=\frac{1}{2}\centerdot 4\centerdot 2=4</math> | ||
| + | = area units. | ||
Revision as of 12:56, 18 September 2008
We can start by drawing the points \displaystyle \left( 1 \right.,\left. 4 \right), \displaystyle \left( 3 \right.,\left. 3 \right) and \displaystyle \left( 1 \right.,\left. 0 \right) in a coordinate system and draw lines between them, so that we get a picture of how thetriangle looks.
If we now think of how we should use the fact that the area of a triangle is given by the formula
Area= \displaystyle \frac{1}{2} (base)∙(height),
it is clear that it is most appropriate to use the edge from \displaystyle \left( 1 \right.,\left. 0 \right) to \displaystyle \left( 1 \right.,\left. 4 \right) as the base of the triangle. The base is then parallel with the y-axis and we can read off its length as the difference in the
\displaystyle y -coordinate between the corner points \displaystyle \left( 1 \right.,\left. 0 \right) and \displaystyle \left( 1 \right.,\left. 4 \right), i.e.
base \displaystyle =4-0=0. In addition, the triangle's height is the horizontal distance from the third corner point \displaystyle \left( 3 \right.,\left. 3 \right) to the base and we can read that off as the difference in the \displaystyle x -direction between \displaystyle \left( 3 \right.,\left. 3 \right) and the line \displaystyle x=1, i.e.
height \displaystyle =3-1=2.
Thus, the triangle's area is
Area= \displaystyle \frac{1}{2} (base)∙(height) \displaystyle =\frac{1}{2}\centerdot 4\centerdot 2=4 = area units.