Solution 1.1:5c
From Förberedande kurs i matematik 1
m (Lösning 1.1:5c moved to Solution 1.1:5c: Robot: moved page) |
|||
| Line 1: | Line 1: | ||
| - | {{ | + | It is quite easy to see that |
| - | < | + | |
| - | < | + | |
| - | {{ | + | <math>\begin{align} |
| + | & \frac{1}{2}=0.5 \\ | ||
| + | & \\ | ||
| + | & \frac{2}{3}=2\centerdot \frac{1}{3}=0.666... \\ | ||
| + | & \\ | ||
| + | & \frac{3}{5}=3\centerdot \frac{1}{5}=3\centerdot 0.2=0.6 \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | <math></math> | ||
| + | |||
| + | |||
| + | which means that | ||
| + | |||
| + | |||
| + | <math>{1}/{2<{3}/{5<{2}/{3}\;}\;}\;</math> . | ||
| + | |||
| + | Because it is more difficult to evaluate the decimal expansion of | ||
| + | <math>{5}/{8}\;</math> | ||
| + | and | ||
| + | <math>{21}/{34}\;</math>, we compare instead | ||
| + | <math>{5}/{8}\;</math> | ||
| + | and | ||
| + | <math>{21}/{34}\;</math> | ||
| + | with | ||
| + | <math>{1}/{2,\ \ {3}/{5}\;}\;</math> and | ||
| + | <math>{2}/{3}\;</math> | ||
| + | by rewriting the fractions so that they have a common denominator. We start by comparing | ||
| + | <math>{5}/{8}\;</math> | ||
| + | with | ||
| + | <math>{1}/{2,\ \ {3}/{5}\;}\;</math> | ||
| + | and | ||
| + | <math>{2}/{3}\;</math> | ||
| + | |||
| + | |||
| + | * We have | ||
| + | <math>\frac{1}{2}=\frac{1\centerdot 4}{2\centerdot 4}=\frac{4}{8}</math> | ||
| + | and thus | ||
| + | <math>\frac{1}{2}<\frac{5}{8}</math> | ||
| + | . | ||
| + | |||
| + | * Then, we have | ||
| + | <math>\frac{3}{5}=\frac{3\centerdot 8}{5\centerdot 8}=\frac{24}{40}</math> | ||
| + | and | ||
| + | <math>\frac{5}{8}=\frac{5\centerdot 5}{8\centerdot 5}=\frac{25}{40}</math> | ||
| + | , which gives that | ||
| + | <math>\frac{3}{5}<\frac{5}{8}</math>. | ||
| + | |||
| + | * Finally, | ||
| + | <math>\frac{2}{3}=\frac{2\centerdot 8}{3\centerdot 8}=\frac{16}{24}</math> | ||
| + | and | ||
| + | <math>\frac{5}{8}=\frac{5\centerdot 3}{8\centerdot 3}=\frac{15}{24}</math>, and this gives that | ||
| + | <math>\frac{5}{8}<\frac{2}{3}</math>. | ||
| + | |||
| + | Thus, | ||
| + | <math>{1}/{2}\;<{3}/{5}\;<{5}/{8}\;<{2}/{3}\;</math>. | ||
| + | |||
| + | When we compare | ||
| + | <math>{21}/{34}\;</math> | ||
| + | with | ||
| + | <math>{1}/{2,\ \ {3}/{5}\;}\;</math> | ||
| + | and | ||
| + | <math>{2}/{3}\;</math>, we obtain: | ||
| + | |||
| + | * because | ||
| + | <math>\frac{1}{2}=\frac{1\centerdot 17}{2\centerdot 17}=\frac{17}{34}</math>, so | ||
| + | <math>\frac{1}{2}<\frac{21}{34}</math> | ||
| + | |||
| + | |||
| + | * furthermore, | ||
| + | <math>\frac{3}{5}=\frac{3\centerdot 34}{5\centerdot 34}=\frac{102}{170}</math> | ||
| + | and | ||
| + | <math>\frac{21}{34}=\frac{21\centerdot 5}{34\centerdot 5}=\frac{105}{170}</math>, i.e. | ||
| + | <math>\frac{3}{5}<\frac{21}{34}</math>. | ||
| + | |||
| + | * we have | ||
| + | <math>\frac{5}{8}=\frac{5\centerdot 17}{8\centerdot 17}=\frac{85}{136}</math> | ||
| + | and | ||
| + | <math>\frac{21}{34}=\frac{21\centerdot 4}{34\centerdot 4}=\frac{84}{136}</math>, which gives that | ||
| + | <math>\frac{21}{34}<\frac{5}{8}</math>. | ||
| + | |||
| + | The answer is | ||
| + | <math>{1}/{2}\;<{3}/{5}\;<{21}/{34}\;<{5}/{8}\;<{2}/{3}\;</math>. | ||
Current revision
It is quite easy to see that
 532=2
532=2 31=0
31=0 666
666

 53=3
53=3 51=3
51=3 0
0 2=0
2=0 6
6
which means that
 2
2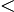 3
3 5
5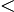 2
2 3
3
Because it is more difficult to evaluate the decimal expansion of
 8
8 34
34 8
8 34
34 2
2 3
3 5
5 3
3 8
8 2
2 3
3 5
5 3
3
- We have
 41
41 4=84
4=84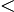 85
85
- Then, we have
 83
83 8=4024
8=4024 55
55 5=4025
5=4025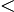 85
85
- Finally,
 82
82 8=2416
8=2416 35
35 3=2415
3=2415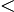 32
32
Thus,
 2
2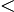 3
3 5
5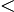 5
5 8
8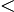 2
2 3
3
When we compare
 34
34 2
2 3
3 5
5 3
3
- because
 171
171 17=3417
17=3417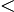 3421
3421
- furthermore,
 343
343 34=170102
34=170102 521
521 5=170105
5=170105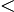 3421
3421
- we have
 175
175 17=85136
17=85136 421
421 4=84136
4=84136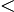 85
85
The answer is \displaystyle {1}/{2}\;<{3}/{5}\;<{21}/{34}\;<{5}/{8}\;<{2}/{3}\;.
