Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
jsMath

Solution 3.4:2a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 3.4:2a moved to Solution 3.4:2a: Robot: moved page)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
The left-hand side is "
-
<center> [[Image:3_4_2a.gif]] </center>
+
<math>\text{2}</math>
-
{{NAVCONTENT_STOP}}
+
raised to something", and therefore a positive number regardless of whatever value the exponent has. We can therefore take the log of both sides,
 +
 
 +
 
 +
<math>\ln 2^{x^{2}-2}=\ln 1</math>
 +
 
 +
and use the log law
 +
<math>\lg a^{b}=b\centerdot \lg a</math>
 +
to get the exponent
 +
<math>x^{\text{2}}-\text{2 }</math>
 +
as a factor on the left-hand side
 +
 
 +
 
 +
<math>\left( x^{\text{2}}-\text{2 } \right)\ln 2=\ln 1</math>
 +
 
 +
 
 +
Because
 +
<math>e^{0}=1</math>, so
 +
<math>\text{ln 1}=0</math>, giving:
 +
 
 +
 
 +
<math>\left( x^{\text{2}}-\text{2 } \right)\ln 2=0</math>
 +
 
 +
 
 +
This means that
 +
<math>x</math>
 +
must satisfy the second-degree equation
 +
 
 +
 
 +
<math>\left( x^{\text{2}}-\text{2 } \right)=0</math>
 +
 
 +
 
 +
Taking the root gives
 +
<math>x=-\sqrt{2}</math>
 +
or
 +
<math>x=\sqrt{2}.</math>
 +
 
 +
 
 +
NOTE: the exercise is taken from a Finnish upper-secondary final examination from March 2007.

Revision as of 10:11, 26 September 2008

The left-hand side is " 2 raised to something", and therefore a positive number regardless of whatever value the exponent has. We can therefore take the log of both sides,


ln2x2−2=ln1

and use the log law lgab=blga to get the exponent x2−2 as a factor on the left-hand side


x2−2 ln2=ln1 


Because e0=1, so ln 1=0, giving:


x2−2 ln2=0 


This means that x must satisfy the second-degree equation


x2−2 =0 


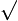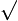Taking the root gives x=−2  or x=2 


NOTE: the exercise is taken from a Finnish upper-secondary final examination from March 2007.

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_3.4:2a"