Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Solution 4.4:3a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
m (Lösning 4.4:3a moved to Solution 4.4:3a: Robot: moved page)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
The right-hand side of the equation is a constant, so the equation is in fact a normal trigonometric equation of the type
-
<center> [[Image:4_4_3a.gif]] </center>
+
<math>\text{cos }x=a</math>.
-
{{NAVCONTENT_STOP}}
+
 
 +
In this case, we can see directly that one solution is
 +
<math>x={\pi }/{6}\;</math>. Using the unit circle, it follows that
 +
<math>x=2\pi -{\pi }/{6}\;={11\pi }/{6}\;</math>
 +
is the only other solution between
 +
<math>0</math>
 +
and
 +
<math>\text{2}\pi </math>.
[[Image:4_4_3_a.gif|center]]
[[Image:4_4_3_a.gif|center]]
 +
 +
We obtain all solutions to the equation if we add multiples of
 +
<math>\text{2}\pi </math>
 +
to the two solutions above:
 +
 +
 +
<math>x=\frac{\pi }{6}+2n\pi </math>
 +
and
 +
<math>x=\frac{11\pi }{6}+2n\pi </math>
 +
 +
 +
where
 +
<math>n</math>
 +
is an arbitrary integer.

Revision as of 09:37, 1 October 2008

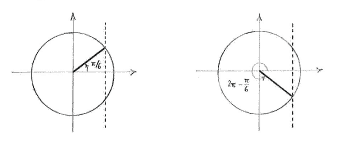
The right-hand side of the equation is a constant, so the equation is in fact a normal trigonometric equation of the type cos x=a.

In this case, we can see directly that one solution is x=6. Using the unit circle, it follows that x=2−6=116 is the only other solution between 0 and 2.

We obtain all solutions to the equation if we add multiples of 2 to the two solutions above:


x=6+2n and x=611+2n


where n is an arbitrary integer.

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.4:3a"