Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Solution 4.2:5a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (11:01, 9 October 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
Because
+
Because <math>135^{\circ} = 90^{\circ} + 45^{\circ}</math>, <math>135^{\circ}</math> is an angle in the second quadrant which makes an angle of <math>45^{\circ}</math> with the positive ''y''-axis.
-
<math>\text{135}^{\circ }\text{ }=\text{ 9}0^{\circ }\text{ }+\text{45}^{\circ }</math>,
+
-
<math>\text{135}^{\circ }\text{ }</math>
+
-
is an angle in the second quadrant which makes an angle of
+
-
<math>\text{45}^{\circ }</math>
+
-
with the positive
+
-
<math>y</math>
+
-
-axis.
+
-
 
+
[[Image:4_2_5_a1.gif|center]]
[[Image:4_2_5_a1.gif|center]]
-
We can determine the point on the unit circle which corresponds to
+
We can determine the point on the unit circle which corresponds to <math>135^{\circ}</math> by introducing an auxiliary triangle and calculating its edges using trigonometry.
-
<math>\text{135}^{\circ }\text{ }</math>
+
-
by introducing an auxiliary triangle and calculating its edges using trigonometry.
+
-
 
+
-
 
+
-
[[Image:4_2_5_a2.gif|center]]
+
-
 
+
-
opposite<math>=1\centerdot \sin \centerdot 45^{\circ }=\frac{1}{\sqrt{2}}</math>
+
-
 
+
-
adjacent
+
-
<math>=1\centerdot \cos \centerdot 45^{\circ }=\frac{1}{\sqrt{2}}</math>
+
 +
{| width="100%"
 +
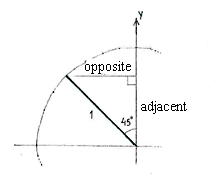
|width="50%" align="center"|[[Image:4_2_5_a2.gif|center]]
 +
|width="50%" align="left"|<math>\begin{align}\text{opposite} &= 1\cdot\sin 45^{\circ} = \dfrac{1}{\sqrt{2}}\\[5pt] \text{adjacent} &= 1\cdot\cos 45^{\circ} = \frac{1}{\sqrt{2}}\end{align}</math>
 +
|}
-
The coordinates of the point are
+
The coordinates of the point are <math>( -1/\!\sqrt{2}, 1/\!\sqrt{2})</math> and this shows that <math>\cos 135^{\circ} = -1/\!\sqrt{2}\,</math>.
-
<math>\left( -\frac{1}{\sqrt{2}} \right.,\left. \frac{1}{\sqrt{2}} \right)</math>
+
-
and this shows that
+
-
<math>\text{cos135}^{\circ }=-\frac{1}{\sqrt{2}}</math>.
+

Current revision

Because 135=90+45, 135 is an angle in the second quadrant which makes an angle of 45 with the positive y-axis.

We can determine the point on the unit circle which corresponds to 135 by introducing an auxiliary triangle and calculating its edges using trigonometry.

oppositeadjacent=1sin45=12=1cos45=12

The coordinates of the point are (−1212)  and this shows that cos135=−12 .

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.2:5a"