Solution 4.3:6a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (07:35, 10 October 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
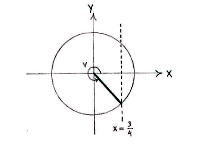
If we think of the angle v as an angle in the unit circle, then
+
If we think of the angle v as an angle in the unit circle, then ''v'' lies in the fourth quadrant and has ''x''-coordinate 3/4.
-
<math>v</math>
+
-
lies in the fourth quadrant and has
+
-
<math>x</math>
+
-
-coordinate
+
-
<math>\frac{3}{4}</math>.
+
-
 
+
[[Image:4_3_6_a1.gif|center]]
[[Image:4_3_6_a1.gif|center]]
-
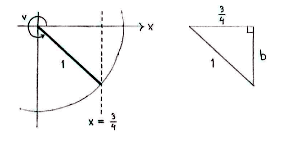
If we enlarge the fourth quadrant, we see that we can make a right-angled triangle with hypotenuse equal to
+
If we enlarge the fourth quadrant, we see that we can make a right-angled triangle with hypotenuse equal to 1 and an opposite side equal to 3/4.
-
<math>\text{1}</math>
+
-
and an opposite side equal to
+
-
<math>\frac{3}{4}</math>.
+
[[Image:4_3_6_a2.gif|center]]
[[Image:4_3_6_a2.gif|center]]
-
Using Pythagoras' theorem, it is possible to determine the remaining side from
+
Using the Pythagorean theorem, it is possible to determine the remaining side from
-
 
+
-
 
+
-
 
+
-
<math>b^{2}+\left( \frac{3}{4} \right)^{2}=1^{2}</math>
+
 +
{{Displayed math||<math>b^2 + \Bigl(\frac{3}{4}\Bigr)^2 = 1^2</math>}}
which gives that
which gives that
 +
{{Displayed math||<math>b = \sqrt{1-\Bigl(\frac{3}{4}\Bigr)^2} = \sqrt{1-\frac{9}{16}} = \sqrt{\frac{7}{16}} = \frac{\sqrt{7}}{4}\,\textrm{.}</math>}}
-
<math>\begin{align}
+
Because the angle ''v'' belongs to the fourth quadrant, its ''y''-coordinate is negative and is therefore equal to <math>-b</math>, i.e.
-
& b^{2}+\left( \frac{3}{4} \right)^{2}=1^{2} \\
+
-
& b=\sqrt{1-\left( \frac{3}{4} \right)^{2}}=\sqrt{1-\frac{9}{16}}=\sqrt{\frac{7}{16}}=\frac{\sqrt{7}}{4} \\
+
-
\end{align}</math>
+
-
 
+
-
 
+
-
Because the angle
+
-
<math>v</math>
+
-
belongs to the fourth quadrant, its
+
-
<math>y</math>
+
-
-coordinate is negative and is therefore equal to
+
-
<math>-b</math>, i.e.
+
-
 
+
-
 
+
-
<math>\sin v=-\frac{\sqrt{7}}{4}</math>
+
 +
{{Displayed math||<math>\sin v=-\frac{\sqrt{7}}{4}\,\textrm{.}</math>}}
Thus, we have directly that
Thus, we have directly that
-
 
+
{{Displayed math||<math>\tan v = \frac{\sin v}{\cos v} = \frac{-\sqrt{7}/4}{3/4} = -\frac{\sqrt{7}}{3}\,\textrm{.}</math>}}
-
<math>\tan v=\frac{\sin v}{\cos v}=\frac{-\frac{\sqrt{7}}{4}}{\frac{3}{4}}=-\frac{\sqrt{7}}{3}</math>
+

Current revision

If we think of the angle v as an angle in the unit circle, then v lies in the fourth quadrant and has x-coordinate 3/4.

If we enlarge the fourth quadrant, we see that we can make a right-angled triangle with hypotenuse equal to 1 and an opposite side equal to 3/4.

Using the Pythagorean theorem, it is possible to determine the remaining side from

\displaystyle b^2 + \Bigl(\frac{3}{4}\Bigr)^2 = 1^2

which gives that

\displaystyle b = \sqrt{1-\Bigl(\frac{3}{4}\Bigr)^2} = \sqrt{1-\frac{9}{16}} = \sqrt{\frac{7}{16}} = \frac{\sqrt{7}}{4}\,\textrm{.}

Because the angle v belongs to the fourth quadrant, its y-coordinate is negative and is therefore equal to \displaystyle -b, i.e.

\displaystyle \sin v=-\frac{\sqrt{7}}{4}\,\textrm{.}

Thus, we have directly that

\displaystyle \tan v = \frac{\sin v}{\cos v} = \frac{-\sqrt{7}/4}{3/4} = -\frac{\sqrt{7}}{3}\,\textrm{.}
Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.3:6a"