Solution 4.4:2c
From Förberedande kurs i matematik 1
(Difference between revisions)
m |
|||
| Line 1: | Line 1: | ||
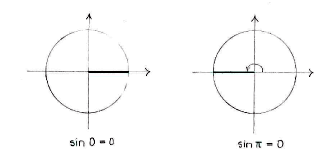
| - | There are two angles in the unit circle, | + | There are two angles in the unit circle, <math>x=0</math> and <math>x=\pi</math>, whose sine has a value of zero. |
| - | <math>x=0 | + | |
| - | and | + | |
| - | <math>x=\pi </math>, whose sine has a value of zero. | + | |
[[Image:4_4_2_c.gif|center]] | [[Image:4_4_2_c.gif|center]] | ||
| - | We get the full solution when we add multiples of | + | We get the full solution when we add multiples of <math>2\pi</math>, |
| - | <math>2\pi </math>, | + | |
| + | {{Displayed math||<math>x = 0+2n\pi\qquad\text{and}\qquad x = \pi + 2n\pi\,,</math>}} | ||
| - | + | where ''n'' is an arbitrary integer. | |
| - | + | ||
| - | + | ||
| - | where | ||
| - | <math>n</math> | ||
| - | is an arbitrary integer. | ||
| - | + | Note: Because the difference between <math>0</math> and <math>\pi</math> is a half turn, the solutions are repeated every half turn and they can be summarized in one expression, | |
| - | <math>0</math> | + | |
| - | and | + | |
| - | <math>\pi </math> | + | |
| - | is a half turn, the solutions are repeated every half turn and they can be summarized in one expression | + | |
| + | {{Displayed math||<math>x=0+n\pi\,,</math>}} | ||
| - | + | where ''n'' is an arbitrary integer. | |
| - | + | ||
| - | + | ||
| - | where | + | |
| - | + | ||
| - | is an arbitrary integer. | + | |
Current revision
There are two angles in the unit circle, \displaystyle x=0 and \displaystyle x=\pi, whose sine has a value of zero.
We get the full solution when we add multiples of \displaystyle 2\pi,
| \displaystyle x = 0+2n\pi\qquad\text{and}\qquad x = \pi + 2n\pi\,, |
where n is an arbitrary integer.
Note: Because the difference between \displaystyle 0 and \displaystyle \pi is a half turn, the solutions are repeated every half turn and they can be summarized in one expression,
| \displaystyle x=0+n\pi\,, |
where n is an arbitrary integer.