Solution 4.4:3a

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (12:49, 13 October 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
The right-hand side of the equation is a constant, so the equation is in fact a normal trigonometric equation of the type
+
The right-hand side of the equation is a constant, so the equation is in fact a normal trigonometric equation of the type <math>\cos x = a\,</math>.
-
<math>\text{cos }x=a</math>.
+
-
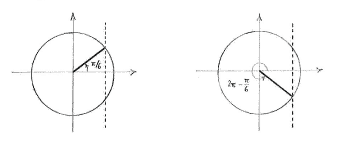
In this case, we can see directly that one solution is
+
In this case, we can see directly that one solution is <math>x = \pi/6\,</math>. Using the unit circle, it follows that <math>x = 2\pi - \pi/6 = 11\pi/6\,</math> is the only other solution between <math>0</math> and <math>2\pi\,</math>.
-
<math>x={\pi }/{6}\;</math>. Using the unit circle, it follows that
+
-
<math>x=2\pi -{\pi }/{6}\;={11\pi }/{6}\;</math>
+
-
is the only other solution between
+
-
<math>0</math>
+
-
and
+
-
<math>\text{2}\pi </math>.
+
[[Image:4_4_3_a.gif|center]]
[[Image:4_4_3_a.gif|center]]
-
We obtain all solutions to the equation if we add multiples of
+
We obtain all solutions to the equation if we add multiples of <math>2\pi</math> to the two solutions above,
-
<math>\text{2}\pi </math>
+
-
to the two solutions above:
+
 +
{{Displayed math||<math>x = \frac{\pi}{6} + 2n\pi\qquad\text{and}\qquad x = \frac{11\pi}{6} + 2n\pi\,,</math>}}
-
<math>x=\frac{\pi }{6}+2n\pi </math>
+
where ''n'' is an arbitrary integer.
-
and
+
-
<math>x=\frac{11\pi }{6}+2n\pi </math>
+
-
 
+
-
 
+
-
where
+
-
<math>n</math>
+
-
is an arbitrary integer.
+

Current revision

The right-hand side of the equation is a constant, so the equation is in fact a normal trigonometric equation of the type \displaystyle \cos x = a\,.

In this case, we can see directly that one solution is \displaystyle x = \pi/6\,. Using the unit circle, it follows that \displaystyle x = 2\pi - \pi/6 = 11\pi/6\, is the only other solution between \displaystyle 0 and \displaystyle 2\pi\,.

We obtain all solutions to the equation if we add multiples of \displaystyle 2\pi to the two solutions above,

\displaystyle x = \frac{\pi}{6} + 2n\pi\qquad\text{and}\qquad x = \frac{11\pi}{6} + 2n\pi\,,

where n is an arbitrary integer.

Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.4:3a"