Solution 4.4:4

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (13:42, 13 October 2008) (edit) (undo)
m
 
Line 1: Line 1:
-
The idea is first to find the general solution to the equation and then to see which angles lie between
+
The idea is first to find the general solution to the equation and then to see which angles lie between <math>0^{\circ}</math> and <math>360^{\circ}\,</math>.
-
<math>0^{\circ }</math>
+
-
and
+
-
<math>360^{\circ }</math>.
+
-
If we start by considering the expression
+
If we start by considering the expression <math>2v+10^{\circ}</math> as an unknown, then we have a usual basic trigonometric equation. One solution which we can see directly is
-
<math>\text{2}v+\text{1}0^{\circ }\text{ }</math>
+
-
as an unknown, then we have a usual basic trigonometric equation. One solution which we can see directly is
+
 +
{{Displayed math||<math>2v + 10^{\circ} = 110^{\circ}\,\textrm{.}</math>}}
-
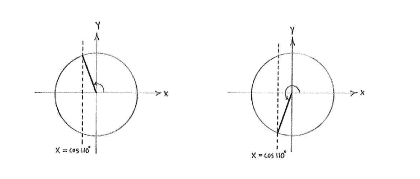
<math>\text{2}v+\text{1}0^{\circ }=110^{\circ }</math>
+
There is then a further solution which satisfies <math>0^{\circ}\le 2v + 10^{\circ}\le 360^{\circ}</math>, where <math>2v+10^{\circ}</math> lies in the third quadrant and makes the same angle with the negative ''y''-axis as <math>100^{\circ}</math> makes with the positive ''y''-axis, i.e. <math>2v + 10^{\circ}</math> makes an angle <math>110^{\circ} - 90^{\circ} = 20^{\circ}</math>
-
 
+
with the negative ''y''-axis and consequently
-
 
+
-
There is then a further solution which satisfies
+
-
<math>0^{\circ }\le \text{2}v+\text{1}0^{\circ }\le \text{36}0^{\circ }</math>, where
+
-
<math>\text{2}v+\text{1}0^{\circ }\text{ }</math>
+
-
lies in the third quadrant and makes the same angle with the negative y-axis as
+
-
<math>\text{1}00^{\circ }</math>
+
-
makes with the positive
+
-
<math>y</math>
+
-
-axis, i.e.
+
-
<math>\text{2}v+\text{1}0^{\circ }\text{ }</math>
+
-
makes an angle
+
-
<math>\text{11}0^{\circ }-\text{9}0^{\circ }=\text{2}0^{\circ }~\text{ }</math>
+
-
with the negative
+
-
<math>y</math>
+
-
-axis and consequently
+
-
 
+
-
 
+
-
<math>\text{2}v+\text{1}0^{\circ }=270^{\circ }-20^{\circ }=250^{\circ }</math>
+
-
 
+
 +
{{Displayed math||<math>2v + 10^{\circ} = 270^{\circ} - 20^{\circ} = 250^{\circ}\,\textrm{.}</math>}}
[[Image:4_4_4.gif|center]]
[[Image:4_4_4.gif|center]]
- 
- 
-
There is then a further solution which satisfies
 
-
<math>0^{\circ }\le \text{2}v+\text{1}0^{\circ }\le \text{36}0^{\circ }</math>, where
 
-
<math>\text{2}v+\text{1}0^{\circ }\text{ }</math>
 
-
lies in the third quadrant and makes the same angle with the negative y-axis as
 
-
<math>\text{1}00^{\circ }</math>
 
-
makes with the positive
 
-
<math>y</math>
 
-
-axis, i.e.
 
-
<math>\text{2}v+\text{1}0^{\circ }\text{ }</math>
 
-
makes an angle
 
-
<math>\text{11}0^{\circ }-\text{9}0^{\circ }=\text{2}0^{\circ }~\text{ }</math>
 
-
with the negative
 
-
<math>y</math>
 
-
-axis and consequently
 
- 
- 
-
<math>\text{2}v+\text{1}0^{\circ }=270^{\circ }-20^{\circ }=250^{\circ }</math>
 
- 
- 
-
FIGURE1 FIGURE2
 
Now it is easy to write down the general solution,
Now it is easy to write down the general solution,
 +
{{Displayed math||<math>\left\{\begin{align} 2v + 10^{\circ} &= 110^{\circ} + n\cdot 360^{\circ}\quad\text{and}\\[5pt] 2v + 10^{\circ} &= 250^{\circ} + n\cdot 360^{\circ}\,,\end{align}\right.</math>}}
-
<math>\text{2}v+\text{1}0^{\circ }=110^{\circ }+n\centerdot 360^{\circ }</math>
+
and if we make ''v'' the subject, we get
-
and
+
-
 
+
-
<math>\text{2}v+\text{1}0^{\circ }=250^{\circ }+n\centerdot 360^{\circ }</math>
+
-
 
+
-
 
+
-
and if we make
+
-
<math>v</math>
+
-
the subject, we get
+
-
 
+
-
 
+
-
<math>v=50^{\circ }+n\centerdot 180^{\circ }</math>
+
-
and
+
-
 
+
-
<math>v=120^{\circ }+n\centerdot 180^{\circ }</math>
+
-
EQ6
+
-
 
+
-
For different values of the integers
+
-
<math>n</math>, we see that the corresponding solutions are:
+
 +
{{Displayed math||<math>\left\{\begin{align} v &= 50^{\circ} + n\cdot 180^{\circ}\quad\text{and}\\[5pt] v &= 120^{\circ} + n\cdot 180^{\circ}\end{align}\right.</math>}}
-
<math>\begin{array}{*{35}l}
+
For different values of the integers ''n'', we see that the corresponding solutions are:
-
\cdots \cdots & \cdots \cdots & \cdots \cdots \\
+
-
n=-2 & v=50^{\circ }-2\centerdot 180^{\circ }=-310^{\circ } & v=120^{\circ }-2\centerdot 180^{\circ }=-240^{\circ } \\
+
-
n=-1 & v=50^{\circ }-1\centerdot 180^{\circ }=-130^{\circ } & v=120^{\circ }-1\centerdot 180^{\circ }=-60^{\circ } \\
+
-
n=0 & v=50^{\circ }+0\centerdot 180^{\circ }=50^{\circ } & v=120^{\circ }+0\centerdot 180^{\circ }=120^{\circ } \\
+
-
n=1 & v=50^{\circ }+1\centerdot 180^{\circ }=230^{\circ } & v=120^{\circ }+1\centerdot 180^{\circ }=300^{\circ } \\
+
-
n=2 & v=50^{\circ }+2\centerdot 180^{\circ }=410^{\circ } & v=120^{\circ }+2\centerdot 180^{\circ }=480^{\circ } \\
+
-
n=3 & v=50^{\circ }+3\centerdot 180^{\circ }=590^{\circ } & v=120^{\circ }+3\centerdot 180^{\circ }=660^{\circ } \\
+
-
\cdots \cdots & \cdots \cdots & \cdots \cdots \\
+
-
\end{array}</math>
+
 +
{| align="center"
 +
|align="center"|<math>\cdots\cdots</math>
 +
||
 +
|align="center"|<math>\cdots\cdots</math>
 +
||
 +
|align="center"|<math>\cdots\cdots</math>
 +
|-
 +
|align="left"|<math>n=-2:</math>
 +
|width="20px"|&nbsp;
 +
|align="left"|<math>v = 50^{\circ} - 2\cdot 180^{\circ} = -310^{\circ}</math>
 +
|width="20px"|&nbsp;
 +
|align="left"|<math>v = 120^{\circ } - 2\cdot 180^{\circ} = -240^{\circ}</math>
 +
|-
 +
|align="left"|<math>n=-1:</math>
 +
||
 +
|align="left"|<math>v = 50^{\circ} - 1\cdot 180^{\circ} = -130^{\circ}</math>
 +
||
 +
|align="left"|<math>v = 120^{\circ} - 1\cdot 180^{\circ} = -60^{\circ}</math>
 +
|-
 +
|align="left"|<math>n=0:</math>
 +
||
 +
|align="left"|<math>v = 50^{\circ} + 0\cdot 180^{\circ} = 50^{\circ}</math>
 +
||
 +
|align="left"|<math>v = 120^{\circ} + 0\cdot 180^{\circ} = 120^{\circ}</math>
 +
|-
 +
|align="left"|<math>n=1:</math>
 +
||
 +
|align="left"|<math>v = 50^{\circ} + 1\cdot 180^{\circ} = 230^{\circ}</math>
 +
||
 +
|align="left"|<math>v = 120^{\circ} + 1\cdot 180^{\circ} = 300^{\circ}</math>
 +
|-
 +
|align="left"|<math>n=2:</math>
 +
||
 +
|align="left"|<math>v = 50^{\circ} + 2\cdot 180^{\circ} = 410^{\circ}</math>
 +
||
 +
|align="left"|<math>v = 120^{\circ} + 2\cdot 180^{\circ} = 480^{\circ}</math>
 +
|-
 +
|align="left"|<math>n=3:</math>
 +
||
 +
|align="left"|<math>v = 50^{\circ} + 3\cdot 180^{\circ} = 590^{\circ}</math>
 +
||
 +
|align="left"|<math>v = 120^{\circ} + 3\cdot 180^{\circ} = 660^{\circ}</math>
 +
|-
 +
|align="center"|<math>\cdots\cdots</math>
 +
||
 +
|align="center"|<math>\cdots\cdots</math>
 +
||
 +
|align="center"|<math>\cdots\cdots</math>
 +
|}
-
From the table, we see that the solutions that are between
 
-
<math>0^{\circ }</math>
 
-
and
 
-
<math>360^{\circ }</math>
 
-
are
 
 +
From the table, we see that the solutions that are between <math>0^{\circ}</math> and <math>360^{\circ}</math> are
-
<math>v=50,\quad v=120^{\circ },\quad v=230^{\circ }</math>
+
{{Displayed math||<math>v = 50^{\circ},\quad v=120^{\circ },\quad v=230^{\circ}\quad\text{and}\quad v=300^{\circ}\,\textrm{.}</math>}}
-
and
+
-
<math>v=300^{\circ }</math>
+

Current revision

The idea is first to find the general solution to the equation and then to see which angles lie between \displaystyle 0^{\circ} and \displaystyle 360^{\circ}\,.

If we start by considering the expression \displaystyle 2v+10^{\circ} as an unknown, then we have a usual basic trigonometric equation. One solution which we can see directly is

\displaystyle 2v + 10^{\circ} = 110^{\circ}\,\textrm{.}

There is then a further solution which satisfies \displaystyle 0^{\circ}\le 2v + 10^{\circ}\le 360^{\circ}, where \displaystyle 2v+10^{\circ} lies in the third quadrant and makes the same angle with the negative y-axis as \displaystyle 100^{\circ} makes with the positive y-axis, i.e. \displaystyle 2v + 10^{\circ} makes an angle \displaystyle 110^{\circ} - 90^{\circ} = 20^{\circ} with the negative y-axis and consequently

\displaystyle 2v + 10^{\circ} = 270^{\circ} - 20^{\circ} = 250^{\circ}\,\textrm{.}

Now it is easy to write down the general solution,

\displaystyle \left\{\begin{align} 2v + 10^{\circ} &= 110^{\circ} + n\cdot 360^{\circ}\quad\text{and}\\[5pt] 2v + 10^{\circ} &= 250^{\circ} + n\cdot 360^{\circ}\,,\end{align}\right.

and if we make v the subject, we get

\displaystyle \left\{\begin{align} v &= 50^{\circ} + n\cdot 180^{\circ}\quad\text{and}\\[5pt] v &= 120^{\circ} + n\cdot 180^{\circ}\end{align}\right.

For different values of the integers n, we see that the corresponding solutions are:


\displaystyle \cdots\cdots \displaystyle \cdots\cdots \displaystyle \cdots\cdots
\displaystyle n=-2:   \displaystyle v = 50^{\circ} - 2\cdot 180^{\circ} = -310^{\circ}   \displaystyle v = 120^{\circ } - 2\cdot 180^{\circ} = -240^{\circ}
\displaystyle n=-1: \displaystyle v = 50^{\circ} - 1\cdot 180^{\circ} = -130^{\circ} \displaystyle v = 120^{\circ} - 1\cdot 180^{\circ} = -60^{\circ}
\displaystyle n=0: \displaystyle v = 50^{\circ} + 0\cdot 180^{\circ} = 50^{\circ} \displaystyle v = 120^{\circ} + 0\cdot 180^{\circ} = 120^{\circ}
\displaystyle n=1: \displaystyle v = 50^{\circ} + 1\cdot 180^{\circ} = 230^{\circ} \displaystyle v = 120^{\circ} + 1\cdot 180^{\circ} = 300^{\circ}
\displaystyle n=2: \displaystyle v = 50^{\circ} + 2\cdot 180^{\circ} = 410^{\circ} \displaystyle v = 120^{\circ} + 2\cdot 180^{\circ} = 480^{\circ}
\displaystyle n=3: \displaystyle v = 50^{\circ} + 3\cdot 180^{\circ} = 590^{\circ} \displaystyle v = 120^{\circ} + 3\cdot 180^{\circ} = 660^{\circ}
\displaystyle \cdots\cdots \displaystyle \cdots\cdots \displaystyle \cdots\cdots


From the table, we see that the solutions that are between \displaystyle 0^{\circ} and \displaystyle 360^{\circ} are

\displaystyle v = 50^{\circ},\quad v=120^{\circ },\quad v=230^{\circ}\quad\text{and}\quad v=300^{\circ}\,\textrm{.}
Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_4.4:4"