Solution 4.4:4
From Förberedande kurs i matematik 1
The idea is first to find the general solution to the equation and then to see which angles lie between \displaystyle 0^{\circ } and \displaystyle 360^{\circ }.
If we start by considering the expression \displaystyle \text{2}v+\text{1}0^{\circ }\text{ } as an unknown, then we have a usual basic trigonometric equation. One solution which we can see directly is
\displaystyle \text{2}v+\text{1}0^{\circ }=110^{\circ }
There is then a further solution which satisfies
\displaystyle 0^{\circ }\le \text{2}v+\text{1}0^{\circ }\le \text{36}0^{\circ }, where
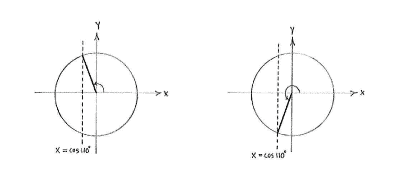
\displaystyle \text{2}v+\text{1}0^{\circ }\text{ }
lies in the third quadrant and makes the same angle with the negative y-axis as
\displaystyle \text{1}00^{\circ }
makes with the positive
\displaystyle y
-axis, i.e.
\displaystyle \text{2}v+\text{1}0^{\circ }\text{ }
makes an angle
\displaystyle \text{11}0^{\circ }-\text{9}0^{\circ }=\text{2}0^{\circ }~\text{ }
with the negative
\displaystyle y
-axis and consequently
\displaystyle \text{2}v+\text{1}0^{\circ }=270^{\circ }-20^{\circ }=250^{\circ }
There is then a further solution which satisfies
\displaystyle 0^{\circ }\le \text{2}v+\text{1}0^{\circ }\le \text{36}0^{\circ }, where
\displaystyle \text{2}v+\text{1}0^{\circ }\text{ }
lies in the third quadrant and makes the same angle with the negative y-axis as
\displaystyle \text{1}00^{\circ }
makes with the positive
\displaystyle y
-axis, i.e.
\displaystyle \text{2}v+\text{1}0^{\circ }\text{ }
makes an angle
\displaystyle \text{11}0^{\circ }-\text{9}0^{\circ }=\text{2}0^{\circ }~\text{ }
with the negative
\displaystyle y
-axis and consequently
\displaystyle \text{2}v+\text{1}0^{\circ }=270^{\circ }-20^{\circ }=250^{\circ }
FIGURE1 FIGURE2
Now it is easy to write down the general solution,
\displaystyle \text{2}v+\text{1}0^{\circ }=110^{\circ }+n\centerdot 360^{\circ }
and
\displaystyle \text{2}v+\text{1}0^{\circ }=250^{\circ }+n\centerdot 360^{\circ }
and if we make
\displaystyle v
the subject, we get
\displaystyle v=50^{\circ }+n\centerdot 180^{\circ }
and
\displaystyle v=120^{\circ }+n\centerdot 180^{\circ } EQ6
For different values of the integers \displaystyle n, we see that the corresponding solutions are:
\displaystyle \begin{array}{*{35}l}
\cdots \cdots & \cdots \cdots & \cdots \cdots \\
n=-2 & v=50^{\circ }-2\centerdot 180^{\circ }=-310^{\circ } & v=120^{\circ }-2\centerdot 180^{\circ }=-240^{\circ } \\
n=-1 & v=50^{\circ }-1\centerdot 180^{\circ }=-130^{\circ } & v=120^{\circ }-1\centerdot 180^{\circ }=-60^{\circ } \\
n=0 & v=50^{\circ }+0\centerdot 180^{\circ }=50^{\circ } & v=120^{\circ }+0\centerdot 180^{\circ }=120^{\circ } \\
n=1 & v=50^{\circ }+1\centerdot 180^{\circ }=230^{\circ } & v=120^{\circ }+1\centerdot 180^{\circ }=300^{\circ } \\
n=2 & v=50^{\circ }+2\centerdot 180^{\circ }=410^{\circ } & v=120^{\circ }+2\centerdot 180^{\circ }=480^{\circ } \\
n=3 & v=50^{\circ }+3\centerdot 180^{\circ }=590^{\circ } & v=120^{\circ }+3\centerdot 180^{\circ }=660^{\circ } \\
\cdots \cdots & \cdots \cdots & \cdots \cdots \\
\end{array}
From the table, we see that the solutions that are between \displaystyle 0^{\circ } and \displaystyle 360^{\circ } are
\displaystyle v=50,\quad v=120^{\circ },\quad v=230^{\circ }
and
\displaystyle v=300^{\circ }