Processing Math: Done

From Förberedande kurs i matematik 1

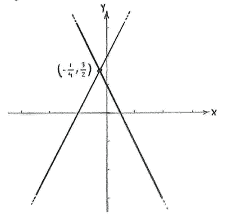
The lines have a point of intersection at that point which simultaneously satisfies the equations of both lines

2x+y−1=0andy−2x−2=0.

If we make y the subject of the second equation y=2x+2 and substitute it into the first equation, we obtain an equation which only contains x,

2x+(2x+2)−1=04x+1=0

which gives that x=−14. Then, from the relation y=2x+2, we obtain y=2(−14)+2=32.

The point of intersection is −4123 .

We check for safety's sake that −4123  really satisfies both equations:

• 2x + y - 1 = 0: LHS=2−41+23−1=−21+23−22=0=RHS. 

• y - 2x - 2 = 0: LHS=23−2−41−2=23+21−24=0=RHS.