Solution 4.2:5a
From Förberedande kurs i matematik 1
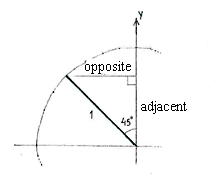
Because \displaystyle \text{135}^{\circ }\text{ }=\text{ 9}0^{\circ }\text{ }+\text{45}^{\circ }, \displaystyle \text{135}^{\circ }\text{ } is an angle in the second quadrant which makes an angle of \displaystyle \text{45}^{\circ } with the positive \displaystyle y -axis.
We can determine the point on the unit circle which corresponds to \displaystyle \text{135}^{\circ }\text{ } by introducing an auxiliary triangle and calculating its edges using trigonometry.
opposite\displaystyle =1\centerdot \sin \centerdot 45^{\circ }=\frac{1}{\sqrt{2}}
adjacent \displaystyle =1\centerdot \cos \centerdot 45^{\circ }=\frac{1}{\sqrt{2}}
The coordinates of the point are
\displaystyle \left( -\frac{1}{\sqrt{2}} \right.,\left. \frac{1}{\sqrt{2}} \right)
and this shows that
\displaystyle \text{cos135}^{\circ }=-\frac{1}{\sqrt{2}}.