Processing Math: Done

From Förberedande kurs i matematik 1

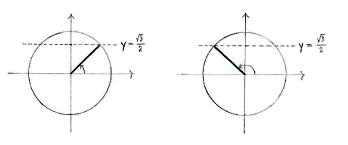
We draw a unit circle and mark on those angles on the circle which have a y -coordinate of 32 , in order to see which solutions lie between 0 and 2.

In the first quadrant, we recognize x=3 as the angle which has a sine value of 32  and then we have the reflectionally symmetric solution x=−3=32 in the second quadrant.

Each of those solutions returns to itself after every revolution, so that we obtain the complete solution if we add multiples of 2

x=3+2n and x=32+2n

where n is an arbitrary integer.

NOTE: when we write that the complete solution is given by

x=3+2n and x=32+2n,

this means that for every integer n, we obtain a solution to the equation:

n=0n=−1n=1n=−2n=2x=3x=3+−12x=3+12x=3+−22x=3+22x=32x=32+−12x=32+12x=32+−22x=32+22

and so on.