Processing Math: 76%

From Förberedande kurs i matematik 1

Let's first investigate when the equality

tanu=tanv

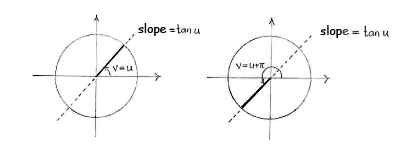
is satisfied. Because u can be interpreted as the slope (gradient) of the line which makes an angle u with the positive x -axis, we see that for a fixed value of tan u, there are two angles v in the unit circle with this slope:

v=u and v=u+

slope = tan u slope = tan u

The angle v has the same slope after every half turn, so if we add multiples of to u, we will obtain all the angles v which satisfy the equality

v=u+n

where n is an arbitrary integer.

If we apply this result to the equation

tanx=tan4x

we see that the solutions are given by

\displaystyle 4x=x+n\pi ( \displaystyle n an arbitrary integer),

and solving for \displaystyle x gives

\displaystyle x=\frac{1}{3}n\pi ( \displaystyle n an arbitrary integer).