Solution 3.4:3c
From Förberedande kurs i matematik 1
With the log laws, we can write the left-hand side as one logarithmic expression,
 |
but this rewriting presupposes that the expressions 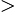 0
0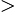 0
0
we must remember to permit only solutions that satisfy 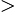 0
0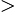 0
0
The equation rewritten in this way is, in turn, only satisfied if the arguments
We rewrite this equation as
 =0 =0 |
which means that 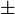 2
2
Because \displaystyle x=-3 is negative, we neglect it, whilst for \displaystyle x=1 we have both that \displaystyle x > 0 and \displaystyle x(x+4) = 2x+3 > 0\,. Therefore, the answer is \displaystyle x=1\,.
