Solution 4.3:6a
From Förberedande kurs i matematik 1
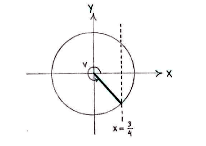
If we think of the angle v as an angle in the unit circle, then v lies in the fourth quadrant and has x-coordinate 3/4.
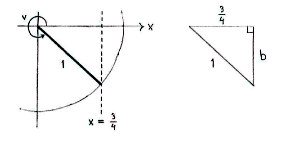
If we enlarge the fourth quadrant, we see that we can make a right-angled triangle with hypotenuse equal to 1 and an opposite side equal to 3/4.
Using the Pythagorean theorem, it is possible to determine the remaining side from
| \displaystyle b^2 + \Bigl(\frac{3}{4}\Bigr)^2 = 1^2 |
which gives that
| \displaystyle b = \sqrt{1-\Bigl(\frac{3}{4}\Bigr)^2} = \sqrt{1-\frac{9}{16}} = \sqrt{\frac{7}{16}} = \frac{\sqrt{7}}{4}\,\textrm{.} |
Because the angle v belongs to the fourth quadrant, its y-coordinate is negative and is therefore equal to \displaystyle -b, i.e.
| \displaystyle \sin v=-\frac{\sqrt{7}}{4}\,\textrm{.} |
Thus, we have directly that
| \displaystyle \tan v = \frac{\sin v}{\cos v} = \frac{-\sqrt{7}/4}{3/4} = -\frac{\sqrt{7}}{3}\,\textrm{.} |