Processing Math: Done
Solution 4.4:8a
From Förberedande kurs i matematik 1
If we use the formula for double angles,
 2cosx=0. 2cosx=0. |
Then, we see that we can take a factor
 2)=0 2)=0 |
and hence divide up the equation into two cases. The equation is satisfied either if  2=0
2=0
This equation has the general solution
 2+n 2+n |
 2=0
2=0
If we collect 
 2
2
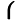 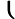 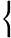   xx= xx= 4+2n 4+2n  =43 =43 +2n +2n  |
where n is an arbitrary integer.
The complete solution of the equation is
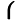 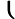 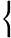           xxx= xxx= 4+2n 4+2n  = = 2+n 2+n  =43 =43 +2n +2n  |
where n is an arbitrary integer.
