Processing Math: Done
Lösning 5.2:7
FörberedandeFysik
Magn. kraften och centripetalkraften ger  R=pqB
R=pqB
Relativistiska räkningar ger
där
Eftersom 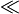 m0c2
m0c2 p=
p=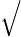 2mEK
2mEK
varför 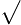 2mEK
2mEK
 6
6 10−19
10−19 1
1 37
37 10−3
10−3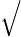 2
2 9
9 1
1 10−31
10−31 20
20 103
103 1
1 6
6 10−19m
10−19m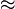 0
0 35m
35m
Relativistiska räkningar ger samma resultat
