5.2 Relativistiska storheter
FörberedandeFysik
(Ny sida: __NOTOC__ {|border="0" cellspacing="0" cellpadding="0" height="30" width="100%" | style="border-bottom:1px solid #797979" width="5px" | {{Mall:Vald flik|[[5.2 Relativistiska storhet...) |
|||
| (11 mellanliggande versioner visas inte.) | |||
| Rad 25: | Rad 25: | ||
:* Definiera relativistiska energin och Einsteins relation | :* Definiera relativistiska energin och Einsteins relation | ||
:* Kunna räkna på enkla exempel med energi och rörelsemängd</div> | :* Kunna räkna på enkla exempel med energi och rörelsemängd</div> | ||
| + | |||
| + | FÖRFATTARE: Göran Tranströmer och Lars-Erik Berg. EDITERARE: Johan Laine | ||
| + | |||
| + | =Relativistisk rörelsemängd= | ||
| + | |||
| + | I klassisk fysik definierar vi rörelsemängden <math>p</math> genom ekvationen <math>p=mv</math>. Einstein visade dock att det korrekta uttrycket är, | ||
| + | |||
| + | <math>p=\gamma mv</math>. | ||
| + | |||
| + | Notera återigen att när hastigheten är låg är <math>\gamma \approx 1</math>, så att <math>p \approx mv</math>, i enlighet med den klassiska fysiken. | ||
| + | |||
| + | Lagen om den totala rörelsemängdens bevarande gäller fortfarande men får ett annat utseende när vi räknar relativistiskt. Eftersom <math>p = \gamma mv</math> får vi nu istället | ||
| + | |||
| + | <math>\sum \gamma mv = \text{konstant}</math>, | ||
| + | |||
| + | och inte som förut att <math>\sum mv = \text{konstant}</math>. Vi får olika konstanter om vi befinner oss i olika inertialsystem, men det gäller alltid att den totala rörelsemängden är konstant. | ||
| + | |||
| + | ==Exempel - rörelsemängdens bevarande== | ||
| + | |||
| + | [[Bild:kap5.2-kollision.gif]] | ||
| + | |||
| + | Vi har en oelastisk stöt mellan en kropp med vilomassa 2 kg och en kropp med vilomassa 1 kg. Kropparna rör sig mot varandra med hastigheten <math>\frac{c}{\sqrt2}</math>. Efter krocken har vi istället en kropp med vilomassa 3 kg. Vilken hastighet kommer den nya kroppen ha? | ||
| + | |||
| + | <b>Relativistisk lösning:</b> | ||
| + | |||
| + | Vi vet att <math>p_{tot}=\sum \gamma mv=konstant</math>, alltså | ||
| + | |||
| + | <math>\displaystyle p_{tot}=\sum \gamma mv = \sum \frac{mv}{\sqrt{1-v^2/c^2}} =\frac{2 \, \textrm{kg} \cdot \frac{c}{\sqrt{2}}}{\sqrt{1-1/2}}+\frac{1 \, \textrm{kg} \cdot (-\frac{c}{\sqrt{2}})}{\sqrt{1-1/2}}=(2-1)c \, \textrm{kg}=c \, \textrm{kg}</math> | ||
| + | |||
| + | Eftersom rörelsemängden är konstant så kommer vi efter kollisionen ha ekvationen | ||
| + | |||
| + | <math> \displaystyle p_{tot}=\sum \gamma mv' = \frac{3 \, \textrm{kg} \cdot v'}{\sqrt{1-(v'/c)^2}}</math> | ||
| + | |||
| + | varifrån vi kan lösa ut <math>v'</math> som | ||
| + | <math>v'=\displaystyle\frac{p_{tot}}{\sqrt{m^2+p_{tot}^2/c^2}}=\frac{c}{\sqrt{3^2+1}}=\frac{c}{\sqrt{10}} \approx 0,316c.</math> | ||
| + | |||
| + | <b>Inkorrekt icke-relativistisk lösning:</b> | ||
| + | |||
| + | Räknar vi istället icke-relativistiskt får vi att | ||
| + | |||
| + | <math>p_{tot}=\sum mv=2 \, \textrm{kg}\cdot \displaystyle \frac{c}{\sqrt{2}}+1 \, \textrm{kg}\cdot \left(-\frac{c}{\sqrt{2}}\right)=\frac{c}{\sqrt{2}} \, \textrm{kg} \,.</math> | ||
| + | |||
| + | Efter kollisionen | ||
| + | |||
| + | <math>p_{tot} = \sum mv' = 3\, \textrm{kg}\cdot v'. </math> | ||
| + | |||
| + | Då får vi sluthastigheten | ||
| + | |||
| + | <math>v'=\displaystyle \frac{p_{tot}}{m}=\frac{\frac{c}{\sqrt{2}}}{3}=\frac{c}{3\sqrt{2}} \approx 0,236c \,.</math> | ||
| + | |||
| + | Vi ser att den är betydligt lägre än den faktiska hastigheten <math>0,316c</math>. | ||
| + | |||
| + | =Relativistisk energi= | ||
| + | |||
| + | Newtons andra lag lyder | ||
| + | |||
| + | <blockquote>”Rörelseförändringen är proportionell mot kraften, och sker i kraftens riktning.”</blockquote> | ||
| + | |||
| + | vilket vi kan skriva som | ||
| + | |||
| + | <math>\displaystyle F=\frac{dp}{dt} \,.</math> | ||
| + | |||
| + | I klassisk fysik använder vi med gott samvete formeln <math>p=mv</math>, och i de fall då massan inte ändras med tiden får vi att <math>\displaystyle \frac{dp}{dt}=m\frac{dv}{dt}</math>, och alltså den välbekanta formeln <math>F=ma</math>. Nu när vi istället har <math>p=\gamma mv</math> får vi en mer komplicerad kraftekvation eftersom <math>\gamma</math> är tidsberoende. | ||
| + | |||
| + | <math>F=\displaystyle\frac{d(\gamma mv)}{dt}=\frac{d}{dt}\left(\frac{mv}{\sqrt{1-v^2/c^2}}\right)</math> | ||
| + | |||
| + | Eftersom kraftekvationen har ändrats ändras också uttrycket för kinetisk energi. Vi utgår från att partikeln är stillastående vid start så att den kinetiska energin är exakt det arbete som vår kraft uträttar på partikeln. Energi kan allmänt skrivas som kraften integrerat över en sträcka. Vi sätter in vårt resultat från kraftekvationen i integralen och får | ||
| + | |||
| + | <math>E_k = \displaystyle \int F \,ds=\int \frac{d(\gamma mv)}{dt}\, \frac{ds}{dt} dt = \int mv \, d(\gamma v) \,.</math> | ||
| + | |||
| + | Att räkna ut denna integral kräver en del kunskap om integration som vi inte förutsätter, men en fullständig härledning för den intresserade finns på [http://en.wikipedia.org/wiki/Special_relativity#Kinetic_energy Wikipedia]. | ||
| + | Om man utför integrationen får man detta mycket viktiga resultat | ||
| + | |||
| + | <math>E_k=(\gamma-1)mc^2 \,.</math> | ||
| + | |||
| + | Förutom att rörelsemängd bevaras vet vi också att den totala energin bevaras. Eftersom även detta gäller i alla inertialsystem kunde Einstein visa att den totala energin <math>E</math> hos en partikel bestäms av uttrycket | ||
| + | |||
| + | <math>E=\gamma mc^2 \,.</math> | ||
| + | |||
| + | Detta betyder att då en partikel står stilla, det vill säga att <math>\gamma=1</math>, så får vi det berömda sambandet <math>E=mc^2</math>! <math>mc^2</math> är alltså all inre energi, oavsett vilken typ av energi det är och vad det är för sorts partikel. Detta är Einsteins mest berömda formel och leder till | ||
| + | |||
| + | <math>E=E_k+E_0</math> | ||
| + | |||
| + | där vi definierar viloenergin <math>E_0</math> som | ||
| + | |||
| + | <math>E_0=mc^2 \,.</math> | ||
| + | |||
| + | Denna energi är inneboende i varje partikel med massa och det är energi av denna typ som frigörs vid kärnkraftverk, i solen och i atombomber. | ||
| + | |||
| + | ==Exempel - massomvandling== | ||
| + | |||
| + | Det här är ett rent tankeexperiment som aldrig kan ske i verkligheten, men det kan illustrera hur mycket energi som finns lagrad som viloenergi. Vi tänker oss att vi har ett föremål med massan 0,5 g som annihileras (kolliderar och förintas) med ett likadant föremål gjort av antimateria. Det som händer då är att all viloenergi, det vill säga ett gram, omvandlas enligt <math>E_0=mc^2</math>. Om all denna energi förs över till ett bowlingklot med massan <math>6</math> kg, hur hög hastighet får då bowlingklotet? | ||
| + | |||
| + | <b>Lösning:</b> | ||
| + | |||
| + | Den totala massan som omvandlas är <math>1</math> g, så den ökning i kinetisk energi som bowlingklotet kommer få är enligt uppgiften <math>E=mc^2=10^{-3} \,\textrm{kg} \cdot c^2</math>. Vi misstänker att bowlingklotet kommer få en väldigt hög fart så vi räknar relativistiskt för säkerhets skull. Vårt uttryck för kinetisk energi är <math>E_k=(\gamma-1) m_{klot}c^2</math>, vilket leder till att | ||
| + | |||
| + | <math>\gamma = 1+\displaystyle\frac{E_k}{m_{klot} c^2} =1+\frac{1}{6}\cdot 10^{-3} \approx 1,000167 \,.</math> | ||
| + | |||
| + | Vi får då hastigheten | ||
| + | |||
| + | <math>v=c\sqrt{1-\displaystyle\frac{1}{\gamma^2}} \approx 0,018c</math> | ||
| + | |||
| + | vilket är vansinnigt snabbt, det är alltså ungefär <math>5,5 \cdot 10^6</math> m/s. | ||
| + | |||
| + | ==Exempel - viloenergins storlek== | ||
| + | |||
| + | Viloenergin är nästan alltid enormt mycket större än den kinetiska energin. Hur snabbt måste ett föremål röra sig för att den kinetiska energin ska vara lika stor som viloenergin? | ||
| + | |||
| + | '''Lösning:''' | ||
| + | |||
| + | Om <math>E_k=E_0</math> så har vi enligt formlerna att | ||
| + | |||
| + | <math>(\gamma-1)mc^2=mc^2</math> | ||
| + | |||
| + | så att <math>\gamma=2</math>. Bryter vi ut <math>v</math> ur <math>\gamma</math> får vi veta att | ||
| + | |||
| + | <math>v=c\sqrt{1-1/\gamma^2}=\displaystyle\frac{\sqrt{3}}{2}c \approx 0,866c \,.</math> | ||
| + | |||
| + | Notera att detta är helt oberoende av föremålets massa. | ||
| + | |||
| + | =Energitriangeln= | ||
| + | |||
| + | Vi ska nu härleda ett samband mellan energin <math>E</math>, rörelsemängden <math>p</math> och viloenergin <math>E_0</math>. Definitionsmässigt gäller att: | ||
| + | |||
| + | <math>p^2=(\gamma mv)^2=\displaystyle\frac{m^2v^2}{1-\frac{v^2}{c^2}}</math> | ||
| + | |||
| + | Totala energin <math>E=\gamma mc^2</math> uttryckt i rörelsemängden <math>p</math> kan då skrivas | ||
| + | |||
| + | <math>E^2 = (\gamma mc^2)^2 = \displaystyle \frac{m^2c^4}{1-\frac{v^2}{c^2}}= \frac{m^2 c^4}{1 - v^2 / c^2} \left( 1 - \frac{v^2}{c^2} + \frac{v^2}{c^2} \right) == m^2c^4+\frac{m^2c^4}{1-\frac{v^2}{c^2}}\frac{v^2}{c^2}= m^2c^4+p^2c^2=E_0^2+p^2c^2 </math> | ||
| + | |||
| + | |||
| + | där vi utnyttjat vårt uttryck för <math>p^2</math> och att <math>E_0=mc^2</math>. | ||
| + | |||
| + | Detta är en mycket viktig formel kallad energitriangeln, så vi presenterar den igen för tydlighetens skull: | ||
| + | |||
| + | <math>E^2=p^2c^2+m^2c^4=p^2c^2+E_0^2</math> | ||
| + | |||
| + | Vi ser även att eftersom <math>p=\gamma mv</math> och <math>E=\gamma mc^2</math> så är <math>\gamma m=p/v=E/c^2</math>, vilket innebär att | ||
| + | |||
| + | <math>E=\displaystyle\frac{pc^2}{v}</math> | ||
| + | |||
| + | vilket är ett uttryck som är oberoende av massan. Det är ett intressant resultat därför att detta är ett uttryck som gäller även för masslösa partiklar, till skillnad från uttrycken <math>E=\gamma mc^2</math> och <math>p=\gamma mv</math>. Masslösa partiklar har ingen viloenergi och därför får vi från energitriangeln med <math>E_0=0</math> att | ||
| + | |||
| + | <math>E=pc</math> | ||
| + | |||
| + | för masslösa partiklar. Genom att använda <math>E=pc^2/v</math> får vi då också att <math>v=c</math>, det vill säga alla masslösa partiklar rör sig med ljusets hastighet. Men det är också så att enbart masslösa partiklar kan röra sig med ljusets hastighet. | ||
| + | |||
| + | Fotoner är ett viktigt exempel på masslösa partiklar. | ||
| + | |||
| + | =När behöver man räkna relativistiskt?= | ||
| + | |||
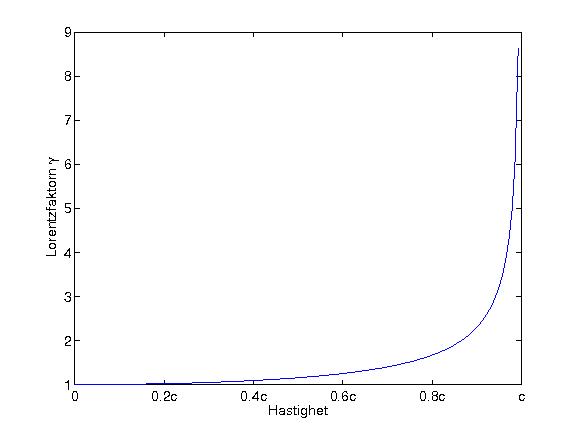
| + | Vid låga hastigheter är <math>\gamma \approx 1<math>, så att <math>p\approx mv</math>. I diagrammet nedan visas värdet av <math>\gamma</math> vid olika hastigheter. I alla praktiska tillämpningar då <math>v</math> är mycket mindre än <math>c</math> kan man alltså lika gärna räkna direkt med <math>p=mv</math>. Hur är det då med energin? <math>E=\gamma mc^2</math> ser inte ut som våra vanliga uttryck. Men man kan visa att för låga hastigheter är <math>E \approx mc^2+mv^2/2</math> där vi genast känner igen den första termen som viloenergi och den andra termen som det klassiska uttrycket för kinetisk energi. Som tumregel brukar man säga att "låga hastigheter" är lägre än <math>0,1c</math>, alltså 10% av ljusets hastighet och då behöver man oftast inte räkna relativistiskt. Vid extremt höga hastighter då vi har <math>v \approx c</math> så gäller <math>E\approx E_k \approx pc</math>. Då <math>v</math> är exakt lika med <math>c</math> gäller som redan nämnt att <math>E=E_k=pc</math>. | ||
| + | |||
| + | [[Bild:5.2-gamma.jpeg]] | ||
| + | |||
| + | =Bestämning av rörelsemängd - praktisk tillämpning= | ||
| + | |||
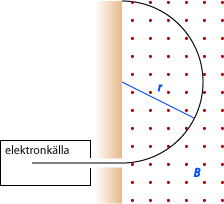
| + | [[Bild:5.2-elektronkalla.gif]] | ||
| + | |||
| + | För att undersöka en laddad, relativistisk partikels rörelse används ofta ett homogent magnetfält som böjer av partikeln i en cirkulär rörelse med radien <math>r</math>. Metoden används i många moderna partikeldetektorer (se även [https://sv.wikipedia.org/wiki/Cyklotron cyklotronen]) eftersom man på så sätt kan bestämma rörelsemängden <math>p</math>, men det är också på så sätt man styr partiklarna. Samma metod används för att styra bläckdropparna i en skrivare till rätt plats. I ett plan vinkelrätt mot magnetfältet gäller sambandet | ||
| + | |||
| + | <math>qvB=\displaystyle \frac{\gamma mv^2}{r}</math> | ||
| + | |||
| + | vilket också ger | ||
| + | |||
| + | <math>p=\gamma mv =qrB</math> | ||
| + | |||
| + | där såväl avböjningens radie <math>r</math> som laddningen <math>q</math> och magnetfältet <math>B</math> kan mätas. | ||
| + | |||
| + | <div class="inforuta" style="width: 580px"> | ||
| + | ===Råd för inläsning=== | ||
| + | |||
| + | ====Tänk på att...==== | ||
| + | |||
| + | Alla känner till gravitationen, men få, utom fysikerna, funderar över den. I dag förs en allt intensivare jakt på gravitonen, den okända partikel som kan förklara gravitationen och som tros resa genom universum som rester av exploderade supernovor. | ||
| + | |||
| + | ====Lästips==== | ||
| + | |||
| + | För dig som behöver en längre förklaring eller vill fördjupa dig ytterligare vil vi tipsa om: | ||
| + | |||
| + | : Halliday and Resnick, Fundamentals of Physics, Wiley Benson, University physics, Wiley kapitel 37 | ||
| + | |||
| + | : [https://sv.wikipedia.org/wiki/Relativitetsteori Läs mer om relativitetsteori på svenska Wikipedia] | ||
| + | |||
| + | ====Länktips==== | ||
| + | |||
| + | : [http://newt.phys.unsw.edu.au/einsteinlight/ Experimentera och lär mer om Einsteins relativitetsteori, multimedia från Univeristy of New South Wales, Sydney Australia] | ||
| + | |||
| + | : [http://www.pbs.org/wgbh/nova/physics/einstein-big-idea.html Läs, lyssna och titta på multimedia om Einsteins relativitetsteori från NOVA "Einstein's Big Idea"] | ||
| + | </div> | ||
Nuvarande version
| Teori | Övningar |
Mål och innehåll
Innehåll
- Relativistisk rörelsemängd
- Relativistisk energi
- Energitriangeln
- När behöver man räkna relativistiskt?
- Bestämning av rörelsemängd - praktisk tillämpning
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Veta när man behöver räkna relativistiskt respektive icke-relativistiskt
- Skilja mellan relativistisk och icke relativistisk energi
- Förklara varför \displaystyle E = E_k = pc för masslösa partiklar
- Definiera relativistiska energin och Einsteins relation
- Kunna räkna på enkla exempel med energi och rörelsemängd
FÖRFATTARE: Göran Tranströmer och Lars-Erik Berg. EDITERARE: Johan Laine
Relativistisk rörelsemängd
I klassisk fysik definierar vi rörelsemängden \displaystyle p genom ekvationen \displaystyle p=mv. Einstein visade dock att det korrekta uttrycket är,
\displaystyle p=\gamma mv.
Notera återigen att när hastigheten är låg är \displaystyle \gamma \approx 1, så att \displaystyle p \approx mv, i enlighet med den klassiska fysiken.
Lagen om den totala rörelsemängdens bevarande gäller fortfarande men får ett annat utseende när vi räknar relativistiskt. Eftersom \displaystyle p = \gamma mv får vi nu istället
\displaystyle \sum \gamma mv = \text{konstant},
och inte som förut att \displaystyle \sum mv = \text{konstant}. Vi får olika konstanter om vi befinner oss i olika inertialsystem, men det gäller alltid att den totala rörelsemängden är konstant.
Exempel - rörelsemängdens bevarande
Vi har en oelastisk stöt mellan en kropp med vilomassa 2 kg och en kropp med vilomassa 1 kg. Kropparna rör sig mot varandra med hastigheten \displaystyle \frac{c}{\sqrt2}. Efter krocken har vi istället en kropp med vilomassa 3 kg. Vilken hastighet kommer den nya kroppen ha?
Relativistisk lösning:
Vi vet att \displaystyle p_{tot}=\sum \gamma mv=konstant, alltså
\displaystyle \displaystyle p_{tot}=\sum \gamma mv = \sum \frac{mv}{\sqrt{1-v^2/c^2}} =\frac{2 \, \textrm{kg} \cdot \frac{c}{\sqrt{2}}}{\sqrt{1-1/2}}+\frac{1 \, \textrm{kg} \cdot (-\frac{c}{\sqrt{2}})}{\sqrt{1-1/2}}=(2-1)c \, \textrm{kg}=c \, \textrm{kg}
Eftersom rörelsemängden är konstant så kommer vi efter kollisionen ha ekvationen
\displaystyle \displaystyle p_{tot}=\sum \gamma mv' = \frac{3 \, \textrm{kg} \cdot v'}{\sqrt{1-(v'/c)^2}}
varifrån vi kan lösa ut \displaystyle v' som \displaystyle v'=\displaystyle\frac{p_{tot}}{\sqrt{m^2+p_{tot}^2/c^2}}=\frac{c}{\sqrt{3^2+1}}=\frac{c}{\sqrt{10}} \approx 0,316c.
Inkorrekt icke-relativistisk lösning:
Räknar vi istället icke-relativistiskt får vi att
\displaystyle p_{tot}=\sum mv=2 \, \textrm{kg}\cdot \displaystyle \frac{c}{\sqrt{2}}+1 \, \textrm{kg}\cdot \left(-\frac{c}{\sqrt{2}}\right)=\frac{c}{\sqrt{2}} \, \textrm{kg} \,.
Efter kollisionen
\displaystyle p_{tot} = \sum mv' = 3\, \textrm{kg}\cdot v'.
Då får vi sluthastigheten
\displaystyle v'=\displaystyle \frac{p_{tot}}{m}=\frac{\frac{c}{\sqrt{2}}}{3}=\frac{c}{3\sqrt{2}} \approx 0,236c \,.
Vi ser att den är betydligt lägre än den faktiska hastigheten \displaystyle 0,316c.
Relativistisk energi
Newtons andra lag lyder
”Rörelseförändringen är proportionell mot kraften, och sker i kraftens riktning.”
vilket vi kan skriva som
\displaystyle \displaystyle F=\frac{dp}{dt} \,.
I klassisk fysik använder vi med gott samvete formeln \displaystyle p=mv, och i de fall då massan inte ändras med tiden får vi att \displaystyle \displaystyle \frac{dp}{dt}=m\frac{dv}{dt}, och alltså den välbekanta formeln \displaystyle F=ma. Nu när vi istället har \displaystyle p=\gamma mv får vi en mer komplicerad kraftekvation eftersom \displaystyle \gamma är tidsberoende.
\displaystyle F=\displaystyle\frac{d(\gamma mv)}{dt}=\frac{d}{dt}\left(\frac{mv}{\sqrt{1-v^2/c^2}}\right)
Eftersom kraftekvationen har ändrats ändras också uttrycket för kinetisk energi. Vi utgår från att partikeln är stillastående vid start så att den kinetiska energin är exakt det arbete som vår kraft uträttar på partikeln. Energi kan allmänt skrivas som kraften integrerat över en sträcka. Vi sätter in vårt resultat från kraftekvationen i integralen och får
\displaystyle E_k = \displaystyle \int F \,ds=\int \frac{d(\gamma mv)}{dt}\, \frac{ds}{dt} dt = \int mv \, d(\gamma v) \,.
Att räkna ut denna integral kräver en del kunskap om integration som vi inte förutsätter, men en fullständig härledning för den intresserade finns på Wikipedia. Om man utför integrationen får man detta mycket viktiga resultat
\displaystyle E_k=(\gamma-1)mc^2 \,.
Förutom att rörelsemängd bevaras vet vi också att den totala energin bevaras. Eftersom även detta gäller i alla inertialsystem kunde Einstein visa att den totala energin \displaystyle E hos en partikel bestäms av uttrycket
\displaystyle E=\gamma mc^2 \,.
Detta betyder att då en partikel står stilla, det vill säga att \displaystyle \gamma=1, så får vi det berömda sambandet \displaystyle E=mc^2! \displaystyle mc^2 är alltså all inre energi, oavsett vilken typ av energi det är och vad det är för sorts partikel. Detta är Einsteins mest berömda formel och leder till
\displaystyle E=E_k+E_0
där vi definierar viloenergin \displaystyle E_0 som
\displaystyle E_0=mc^2 \,.
Denna energi är inneboende i varje partikel med massa och det är energi av denna typ som frigörs vid kärnkraftverk, i solen och i atombomber.
Exempel - massomvandling
Det här är ett rent tankeexperiment som aldrig kan ske i verkligheten, men det kan illustrera hur mycket energi som finns lagrad som viloenergi. Vi tänker oss att vi har ett föremål med massan 0,5 g som annihileras (kolliderar och förintas) med ett likadant föremål gjort av antimateria. Det som händer då är att all viloenergi, det vill säga ett gram, omvandlas enligt \displaystyle E_0=mc^2. Om all denna energi förs över till ett bowlingklot med massan \displaystyle 6 kg, hur hög hastighet får då bowlingklotet?
Lösning:
Den totala massan som omvandlas är \displaystyle 1 g, så den ökning i kinetisk energi som bowlingklotet kommer få är enligt uppgiften \displaystyle E=mc^2=10^{-3} \,\textrm{kg} \cdot c^2. Vi misstänker att bowlingklotet kommer få en väldigt hög fart så vi räknar relativistiskt för säkerhets skull. Vårt uttryck för kinetisk energi är \displaystyle E_k=(\gamma-1) m_{klot}c^2, vilket leder till att
\displaystyle \gamma = 1+\displaystyle\frac{E_k}{m_{klot} c^2} =1+\frac{1}{6}\cdot 10^{-3} \approx 1,000167 \,.
Vi får då hastigheten
\displaystyle v=c\sqrt{1-\displaystyle\frac{1}{\gamma^2}} \approx 0,018c
vilket är vansinnigt snabbt, det är alltså ungefär \displaystyle 5,5 \cdot 10^6 m/s.
Exempel - viloenergins storlek
Viloenergin är nästan alltid enormt mycket större än den kinetiska energin. Hur snabbt måste ett föremål röra sig för att den kinetiska energin ska vara lika stor som viloenergin?
Lösning:
Om \displaystyle E_k=E_0 så har vi enligt formlerna att
\displaystyle (\gamma-1)mc^2=mc^2
så att \displaystyle \gamma=2. Bryter vi ut \displaystyle v ur \displaystyle \gamma får vi veta att
\displaystyle v=c\sqrt{1-1/\gamma^2}=\displaystyle\frac{\sqrt{3}}{2}c \approx 0,866c \,.
Notera att detta är helt oberoende av föremålets massa.
Energitriangeln
Vi ska nu härleda ett samband mellan energin \displaystyle E, rörelsemängden \displaystyle p och viloenergin \displaystyle E_0. Definitionsmässigt gäller att:
\displaystyle p^2=(\gamma mv)^2=\displaystyle\frac{m^2v^2}{1-\frac{v^2}{c^2}}
Totala energin \displaystyle E=\gamma mc^2 uttryckt i rörelsemängden \displaystyle p kan då skrivas
\displaystyle E^2 = (\gamma mc^2)^2 = \displaystyle \frac{m^2c^4}{1-\frac{v^2}{c^2}}= \frac{m^2 c^4}{1 - v^2 / c^2} \left( 1 - \frac{v^2}{c^2} + \frac{v^2}{c^2} \right) == m^2c^4+\frac{m^2c^4}{1-\frac{v^2}{c^2}}\frac{v^2}{c^2}= m^2c^4+p^2c^2=E_0^2+p^2c^2
där vi utnyttjat vårt uttryck för \displaystyle p^2 och att \displaystyle E_0=mc^2.
Detta är en mycket viktig formel kallad energitriangeln, så vi presenterar den igen för tydlighetens skull:
\displaystyle E^2=p^2c^2+m^2c^4=p^2c^2+E_0^2
Vi ser även att eftersom \displaystyle p=\gamma mv och \displaystyle E=\gamma mc^2 så är \displaystyle \gamma m=p/v=E/c^2, vilket innebär att
\displaystyle E=\displaystyle\frac{pc^2}{v}
vilket är ett uttryck som är oberoende av massan. Det är ett intressant resultat därför att detta är ett uttryck som gäller även för masslösa partiklar, till skillnad från uttrycken \displaystyle E=\gamma mc^2 och \displaystyle p=\gamma mv. Masslösa partiklar har ingen viloenergi och därför får vi från energitriangeln med \displaystyle E_0=0 att
\displaystyle E=pc
för masslösa partiklar. Genom att använda \displaystyle E=pc^2/v får vi då också att \displaystyle v=c, det vill säga alla masslösa partiklar rör sig med ljusets hastighet. Men det är också så att enbart masslösa partiklar kan röra sig med ljusets hastighet.
Fotoner är ett viktigt exempel på masslösa partiklar.
När behöver man räkna relativistiskt?
Vid låga hastigheter är \displaystyle \gamma \approx 1. I diagrammet nedan visas värdet av \displaystyle \gamma vid olika hastigheter. I alla praktiska tillämpningar då \displaystyle v är mycket mindre än \displaystyle c kan man alltså lika gärna räkna direkt med \displaystyle p=mv. Hur är det då med energin? \displaystyle E=\gamma mc^2 ser inte ut som våra vanliga uttryck. Men man kan visa att för låga hastigheter är \displaystyle E \approx mc^2+mv^2/2 där vi genast känner igen den första termen som viloenergi och den andra termen som det klassiska uttrycket för kinetisk energi. Som tumregel brukar man säga att "låga hastigheter" är lägre än \displaystyle 0,1c, alltså 10% av ljusets hastighet och då behöver man oftast inte räkna relativistiskt. Vid extremt höga hastighter då vi har \displaystyle v \approx c så gäller \displaystyle E\approx E_k \approx pc. Då \displaystyle v är exakt lika med \displaystyle c gäller som redan nämnt att \displaystyle E=E_k=pc.
Bestämning av rörelsemängd - praktisk tillämpning
För att undersöka en laddad, relativistisk partikels rörelse används ofta ett homogent magnetfält som böjer av partikeln i en cirkulär rörelse med radien \displaystyle r. Metoden används i många moderna partikeldetektorer (se även cyklotronen) eftersom man på så sätt kan bestämma rörelsemängden \displaystyle p, men det är också på så sätt man styr partiklarna. Samma metod används för att styra bläckdropparna i en skrivare till rätt plats. I ett plan vinkelrätt mot magnetfältet gäller sambandet
\displaystyle qvB=\displaystyle \frac{\gamma mv^2}{r}
vilket också ger
\displaystyle p=\gamma mv =qrB
där såväl avböjningens radie \displaystyle r som laddningen \displaystyle q och magnetfältet \displaystyle B kan mätas.
Råd för inläsning
Tänk på att...
Alla känner till gravitationen, men få, utom fysikerna, funderar över den. I dag förs en allt intensivare jakt på gravitonen, den okända partikel som kan förklara gravitationen och som tros resa genom universum som rester av exploderade supernovor.
Lästips
För dig som behöver en längre förklaring eller vill fördjupa dig ytterligare vil vi tipsa om:
- Halliday and Resnick, Fundamentals of Physics, Wiley Benson, University physics, Wiley kapitel 37