3.2 Övningar
FörberedandeFysik
| (8 mellanliggande versioner visas inte.) | |||
| Rad 13: | Rad 13: | ||
| - | a) Vilken är bollens högsta höjd ovanför marken under dess bana, om <math>g= | + | a) Vilken är bollens högsta höjd ovanför marken under dess bana, om <math>g=10\,\mathrm{m/s}^2</math>?<br\> |
b) Efter att bollen har förflyttat sig ett horisontellt avstånd på 36 m träffar den ett fönster, bestäm på vilken höjd <i>h</i> fönstret sitter? | b) Efter att bollen har förflyttat sig ett horisontellt avstånd på 36 m träffar den ett fönster, bestäm på vilken höjd <i>h</i> fönstret sitter? | ||
| Rad 21: | Rad 21: | ||
===Övning 3.2:2=== | ===Övning 3.2:2=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| + | En bil rör sig med konstant fart i en cirkulär bana med radien <math>r=75,0 \,\mathrm{m}</math>. Det tar bilen 30,0 s att fullborda ett varv. | ||
| + | [[Bild:ovning_3_2_2.jpg]] | ||
| + | |||
| + | a)Bestäm storleken på bilens hastighet <math>v</math>.<br\> | ||
| + | |||
| + | b)Efter att bilen har gått 1/3 varv runt banan relativt startpunkten, vilka är <math>x-</math> och <math>y-</math> komponenterna hos bilens hastighet?<br\> | ||
| + | |||
| + | c)Vilka är storleken respektive riktningen hos bilens acceleration då bilen har åkt 1/4 av sin bana? | ||
</div>{{#NAVCONTENT:Svar|Svar 3.2:2|Lösning |Lösning 3.2:2}} | </div>{{#NAVCONTENT:Svar|Svar 3.2:2|Lösning |Lösning 3.2:2}} | ||
| + | |||
| + | |||
| + | |||
===Övning 3.2:3=== | ===Övning 3.2:3=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| + | En boll kastas från marken. Efter 1,5 sekunder har bollen en hastighet som bildar en vinkel på <math>16,0^\circ</math> mot horisonten och en horisontell hastighetskomponent på +25,0 m/s. Vi bortser från luftmotståndet. | ||
| + | a) Vilken är den vertikala komponenten av bollens hastighet efter 1,5 sekunder?<br\> | ||
| + | |||
| + | b) Hur långt har bollen kommit horisontellt från startläget?<br\> | ||
| + | |||
| + | c) Vilken är utgångsfarten, d v s storleken av utgångshastigheten? | ||
</div>{{#NAVCONTENT:Svar|Svar 3.2:3|Lösning |Lösning 3.2:3}} | </div>{{#NAVCONTENT:Svar|Svar 3.2:3|Lösning |Lösning 3.2:3}} | ||
| Rad 33: | Rad 50: | ||
===Övning 3.2:4=== | ===Övning 3.2:4=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| + | [[Bild:ovning_3_2_4.jpg]] | ||
| + | En boll kastas mot en vägg från marken med en hastighet som bildar en vinkel på <math>38,0^\circ</math>. Väggen befinner sig på ett horisontellt avstånd 15,0 m från utgångspunkten och det tar bollen 1,30 sekunder att nå väggen. | ||
| + | |||
| + | a) Vilken är bollens horisontella hastighet?<br\> | ||
| + | |||
| + | b) Vilken är bollens begynnelsefart <math>v_0</math>?<br\> | ||
| + | |||
| + | c) Vid vilken höjd H träffar bollen väggen? | ||
</div>{{#NAVCONTENT:Svar|Svar 3.2:4|Lösning |Lösning 3.2:4}} | </div>{{#NAVCONTENT:Svar|Svar 3.2:4|Lösning |Lösning 3.2:4}} | ||
| Rad 39: | Rad 64: | ||
===Övning 3.2:5=== | ===Övning 3.2:5=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| + | En partikel svänger 270 gånger under en minut under en harmonisk svängningsrörelse. | ||
| + | |||
| + | a) Vilken är rörelsens <math>\omega</math>? Ledtråd: Betrakta en partikel som roterar i en cirkel 270 gånger under en minut.<br\> | ||
| + | |||
| + | b) Vilken är partikelns maximala hastighet om amplituden är 61 cm?<br\> | ||
| + | c) Vilken är den maximala accelerationen? Ledtråd: använd <math>a=\omega ^2y</math>. | ||
</div>{{#NAVCONTENT:Svar|Svar 3.2:5|Lösning |Lösning 3.2:5}} | </div>{{#NAVCONTENT:Svar|Svar 3.2:5|Lösning |Lösning 3.2:5}} | ||
Nuvarande version
| Teori | Övningar |
Övning 3.2:1
En boll kastas från en höjd på 0,8 m ovanför den horisontella marken med en hastighet på u = 26 m/s och en lutning \displaystyle \alpha mot marken, där \displaystyle \tan \alpha =\frac{5}{12}. Vi behandlar bollen som en partikel och bortser ifrån luftmotstånd.
a) Vilken är bollens högsta höjd ovanför marken under dess bana, om \displaystyle g=10\,\mathrm{m/s}^2?
b) Efter att bollen har förflyttat sig ett horisontellt avstånd på 36 m träffar den ett fönster, bestäm på vilken höjd h fönstret sitter?
Övning 3.2:2
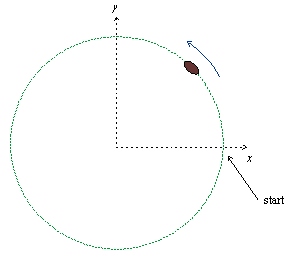
En bil rör sig med konstant fart i en cirkulär bana med radien \displaystyle r=75,0 \,\mathrm{m}. Det tar bilen 30,0 s att fullborda ett varv.
a)Bestäm storleken på bilens hastighet \displaystyle v.
b)Efter att bilen har gått 1/3 varv runt banan relativt startpunkten, vilka är \displaystyle x- och \displaystyle y- komponenterna hos bilens hastighet?
c)Vilka är storleken respektive riktningen hos bilens acceleration då bilen har åkt 1/4 av sin bana?
Övning 3.2:3
En boll kastas från marken. Efter 1,5 sekunder har bollen en hastighet som bildar en vinkel på \displaystyle 16,0^\circ mot horisonten och en horisontell hastighetskomponent på +25,0 m/s. Vi bortser från luftmotståndet.
a) Vilken är den vertikala komponenten av bollens hastighet efter 1,5 sekunder?
b) Hur långt har bollen kommit horisontellt från startläget?
c) Vilken är utgångsfarten, d v s storleken av utgångshastigheten?
Övning 3.2:4
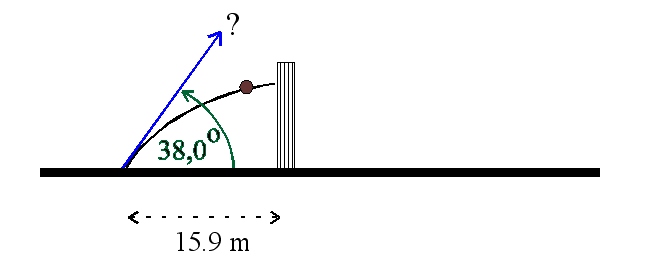
En boll kastas mot en vägg från marken med en hastighet som bildar en vinkel på \displaystyle 38,0^\circ. Väggen befinner sig på ett horisontellt avstånd 15,0 m från utgångspunkten och det tar bollen 1,30 sekunder att nå väggen.
a) Vilken är bollens horisontella hastighet?
b) Vilken är bollens begynnelsefart \displaystyle v_0?
c) Vid vilken höjd H träffar bollen väggen?
Övning 3.2:5
En partikel svänger 270 gånger under en minut under en harmonisk svängningsrörelse.
a) Vilken är rörelsens \displaystyle \omega? Ledtråd: Betrakta en partikel som roterar i en cirkel 270 gånger under en minut.
b) Vilken är partikelns maximala hastighet om amplituden är 61 cm?
c) Vilken är den maximala accelerationen? Ledtråd: använd \displaystyle a=\omega ^2y.
 Hämtar...
Hämtar...