3.4 Övningar
FörberedandeFysik
| (7 mellanliggande versioner visas inte.) | |||
| Rad 10: | Rad 10: | ||
===Övning 3.4:1=== | ===Övning 3.4:1=== | ||
<div class="ovning"> | <div class="ovning"> | ||
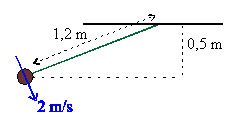
| - | En partikelpendel består av en partikel och en tråd med längd <math>1,2 m</math>.<br\> | + | En partikelpendel består av en partikel och en tråd med längd <math>1,2 \,\mathrm{m}</math>.<br\> |
| - | Den släpps med en fart <math>2 m/s</math> från ett läge <math>0,5 m</math> under upphängningspunkten som i figuren. | + | Den släpps med en fart <math>2 \,\mathrm{m/s}</math> från ett läge <math>0,5 \,\mathrm{m}</math> under upphängningspunkten som i figuren. |
[[Bild:ovning_3_4_1.jpg]] | [[Bild:ovning_3_4_1.jpg]] | ||
| + | a) Vilken är pendelns maximala fart? Anta att <math>g = 10 \,\mathrm{m/s}^2</math><br\> | ||
| + | b) Kan pendeln nå upp till det horisontella läget? | ||
</div>{{#NAVCONTENT:Svar|Svar 3.4:1|Lösning |Lösning 3.4:1}} | </div>{{#NAVCONTENT:Svar|Svar 3.4:1|Lösning |Lösning 3.4:1}} | ||
| Rad 20: | Rad 22: | ||
===Övning 3.4:2=== | ===Övning 3.4:2=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| - | + | En liten boll släpps utan hastighet från en höjd från en höjd <math>3 \,\mathrm{m}</math> ovanför marken. Den studsar mot marken varvid bollens fart minskar med <math>50 \%</math>. Hur högt kommer bollen efter studsen?<br\> | |
| + | (Ledtråd: hur stor andel av sin kinetiska energi förlorar bollen vid studsen?) | ||
</div>{{#NAVCONTENT:Svar|Svar 3.4:2|Lösning |Lösning 3.4:2}} | </div>{{#NAVCONTENT:Svar|Svar 3.4:2|Lösning |Lösning 3.4:2}} | ||
| Rad 26: | Rad 29: | ||
===Övning 3.4:3=== | ===Övning 3.4:3=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| + | En rak väg har en lutningsvinkel <math>\alpha</math> , där <math>\sin\alpha = \frac{1}{20}</math>. En lastbil med massan <math>4800</math> kg rör sig uppför vägen med en konstant fart på <math>12</math> m/s . Luftmotstånd och friktion ger upphov till en total motståndskraft på <math>2000 \,\mathrm{N}</math>. Antag att <math>g = 10\,\mathrm{m/s}^2</math> | ||
| + | |||
| + | |||
| + | a) Vilken är motoreffekten P under denna rörelse, uttryckt i kW?<br\> | ||
| + | (Ledtråd: Vilken är den totala kraften på lastbilen nedför planet?)<br\> | ||
| + | |||
| + | |||
| + | b) Bestäm lastbilens acceleration <math>a</math> i första ögonblick efter att vägen blivit horisontell?<br\> | ||
| + | |||
| + | c) Vilken är lastbilens maximala hastighet då motorn behåller samma effekt hela tiden? | ||
</div>{{#NAVCONTENT:Svar|Svar 3.4:3|Lösning |Lösning 3.4:3}} | </div>{{#NAVCONTENT:Svar|Svar 3.4:3|Lösning |Lösning 3.4:3}} | ||
| Rad 32: | Rad 45: | ||
===Övning 3.4:4=== | ===Övning 3.4:4=== | ||
<div class="ovning"> | <div class="ovning"> | ||
| + | En låda med massan <math>m = 190 \,\mathrm{kg}</math> hissas med hjälp av ett rep upp från marken med en konstant hastighet på <math>3,8 \,\mathrm{m/s}</math>.<br\> Repet drivs av en motor med en konstant effekt på <math>7,3 \,\mathrm{kW}</math>. | ||
| + | a) Hur stor är spännkraften <math>S</math> i repet?<br\> | ||
| + | b) Hur mycket arbete <math>W</math> har motorn uträttat då lådan har lyfts <math>H = 2,9 \,\mathrm{m}</math> över marken?<br\> | ||
| + | c) Hur mycket energi har systemet förlorat då, (vid en höjd <math>2,9 \,\mathrm{m}</math>)? | ||
</div>{{#NAVCONTENT:Svar|Svar 3.4:4|Lösning |Lösning 3.4:4}} | </div>{{#NAVCONTENT:Svar|Svar 3.4:4|Lösning |Lösning 3.4:4}} | ||
Nuvarande version
| Teori | Övningar |
Övning 3.4:1
En partikelpendel består av en partikel och en tråd med längd \displaystyle 1,2 \,\mathrm{m}.
Den släpps med en fart \displaystyle 2 \,\mathrm{m/s} från ett läge \displaystyle 0,5 \,\mathrm{m} under upphängningspunkten som i figuren.
a) Vilken är pendelns maximala fart? Anta att \displaystyle g = 10 \,\mathrm{m/s}^2
b) Kan pendeln nå upp till det horisontella läget?
Övning 3.4:2
En liten boll släpps utan hastighet från en höjd från en höjd \displaystyle 3 \,\mathrm{m} ovanför marken. Den studsar mot marken varvid bollens fart minskar med \displaystyle 50 \%. Hur högt kommer bollen efter studsen?
(Ledtråd: hur stor andel av sin kinetiska energi förlorar bollen vid studsen?)
Övning 3.4:3
En rak väg har en lutningsvinkel \displaystyle \alpha , där \displaystyle \sin\alpha = \frac{1}{20}. En lastbil med massan \displaystyle 4800 kg rör sig uppför vägen med en konstant fart på \displaystyle 12 m/s . Luftmotstånd och friktion ger upphov till en total motståndskraft på \displaystyle 2000 \,\mathrm{N}. Antag att \displaystyle g = 10\,\mathrm{m/s}^2
a) Vilken är motoreffekten P under denna rörelse, uttryckt i kW?
(Ledtråd: Vilken är den totala kraften på lastbilen nedför planet?)
b) Bestäm lastbilens acceleration \displaystyle a i första ögonblick efter att vägen blivit horisontell?
c) Vilken är lastbilens maximala hastighet då motorn behåller samma effekt hela tiden?
Övning 3.4:4
En låda med massan \displaystyle m = 190 \,\mathrm{kg} hissas med hjälp av ett rep upp från marken med en konstant hastighet på \displaystyle 3,8 \,\mathrm{m/s}.
Repet drivs av en motor med en konstant effekt på \displaystyle 7,3 \,\mathrm{kW}.
a) Hur stor är spännkraften \displaystyle S i repet?
b) Hur mycket arbete \displaystyle W har motorn uträttat då lådan har lyfts \displaystyle H = 2,9 \,\mathrm{m} över marken?
c) Hur mycket energi har systemet förlorat då, (vid en höjd \displaystyle 2,9 \,\mathrm{m})?
 Hämtar...
Hämtar...