2.2 Elementär vektoralgebra
FörberedandeFysik
| Rad 157: | Rad 157: | ||
<math>c=c_x+c_y=(a_x+b_x)+(a_y+b_y)</math> | <math>c=c_x+c_y=(a_x+b_x)+(a_y+b_y)</math> | ||
| + | |||
{| class=wikitable border="0" | {| class=wikitable border="0" | ||
| Rad 164: | Rad 165: | ||
| <math>c\cos\gamma =a\cos\alpha + b\cos\beta</math> || || <math>c\sin\gamma =a\sin\alpha + b\sin\beta</math> | | <math>c\cos\gamma =a\cos\alpha + b\cos\beta</math> || || <math>c\sin\gamma =a\sin\alpha + b\sin\beta</math> | ||
|} | |} | ||
| + | |||
I stället för att skriva ut a med basvektorerna a=axex+ayey eller a=acosËex+asinËey så skriver man kortare a=(ax;ay) eller a=(acosË;asinË) med kommatecken mellan komponenterna. | I stället för att skriva ut a med basvektorerna a=axex+ayey eller a=acosËex+asinËey så skriver man kortare a=(ax;ay) eller a=(acosË;asinË) med kommatecken mellan komponenterna. | ||
Versionen från 11 december 2009 kl. 08.49
| Teori | Övningar |
Mål och innehåll
Innehåll
- Vektorbegreppet
- Resultant och komposant
- Längd av vektor och enhetsvektor
- Komponenter
- Nollvektorn
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Definiera begreppen vektor och skalär, belopp (längd) av vektor, resultant, komposant och komponent, enhetsvektor, nollvektorn och basvektor.
- Skilja mellan komposant och komponent.
- Skilja mellan enhetsvektor och basvektor.
- Beskriva skillnader och likheter mellan komposant, enhetsvektor och basvektor.
- Förklara varför man använder sig av vektorer i fysiken och vad som händer om man försöker lösa uppgifter utan att använda vektorer.
- Ställa upp och räkna ut addition av vektorer och multiplikation av vektor med ett reellt tal.
- Ställa upp och räkna ut belopp av vektor, enhetsvektor och resultant.
Vektorbegreppet
I fysiken använder man sig av samband (formler) mellan fysikaliska storheter.
En storhet är en egenskap som kan mätas eller beräknas.
Vissa storheter har enbart storlek; en sådan storhet kallas skalär. Andra storheter har både storlek och riktning; en sådan storhet kallas vektor.
Vektorer kan betecknas på några olika sätt; med fet symbol: a, med pil över: \displaystyle \vec{a}, med streck över: \displaystyle \bar{a} eller med streck under: \displaystyle \underline{a}. I fortsättningen använder vi fet symbol: a.
Storheter som inte har vektoregenskap anges med kursiv stil: a eller \displaystyle {a} (det finns ju faktiskt två olika sätt att skriva a eller \displaystyle {a}, liksom det beroende på typsnitt finns två sätt att skriva g).
En vektor kan multipliceras med ett reellt tal, varvid den blir lika många gånger större (eller mindre om talet är mindre än 1). Multiplikation med ett negativt tal vänder om vektorns riktning:
Resultant och komposant
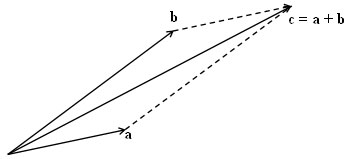
Krafter som verkar i samma punkt kan sammansättas till en resultant. En kraft som ligger till grund för en sådan sammansättning kallas komposant:
Ovan är således a och b komposanter samt c = a + b resultant.
Omvänt kan en kraft uppdelas i komposanter. En speciellt användbar uppdelning får man om man använder rätvinkliga komposanter: I fortsättningen behandlar vi enbart vektorer i xy-planet dvs i två dimensioner. Men det är naturligt att utveckla vektorbegreppet till rummet dvs tre dimensioner och även till ännu högre dimensioner. Vi kommer att använda oss av den tredje dimensionen i samband med moment (se avsnitt 2.4).
\displaystyle a=a_x+a_y \qquad b=b_x+b_y \qquad c=c_x+c_y=a+b=(a_x+b_x)+(a_y+b_y)
Längd av vektor och enhetsvektor
Vi inför nu längden (även kallad beloppet) \displaystyle a av vektorn a som \displaystyle a=|a|.
Inför nu också enhetsvektorerna \displaystyle e_x och \displaystyle e_y som har egenskapen att deras längd är 1 och att de är parallella med x- resp. y-axeln:
- \displaystyle |e_x|=1 \qquad |e_y|=1
Komponenter
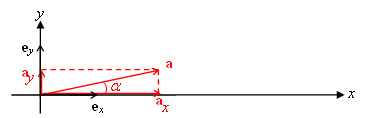
Samtidigt inför vi komponenten \displaystyle a_x av vektorn a som den rätvinkliga projektionen av vektorn a på x-axeln dvs:
\displaystyle a_x=a\cos\alpha
På motsvarande sätt införs komponenten \displaystyle a_y av vektorn a som den rätvinkliga projektionen av a på y-axeln dvs:
\displaystyle a_y=a\sin\alpha
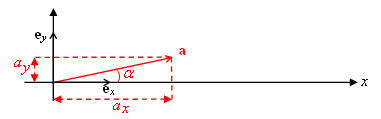
Den rätvinliga projektionen på en axel framgår av figuren ovan, när man drar en linje vinkelrät mot axeln till vektorns spets. Om fotpunkten inte går genom origo, drar man på samma sätt en linje vinklerät mot axeln genom vektorns fotpunkt. Avståndet på axeln mellan de två dragna linjerna (eller mellan origo och den dragna linjen) är då vektorns projektion på axeln.
Observera att följande gäller:
| \displaystyle \alpha=0 | \displaystyle \sin\alpha=0 | \displaystyle \cos\alpha=1 | ||
| \displaystyle 0<\alpha<\frac{\pi}{2} | \displaystyle \sin\alpha>0 | \displaystyle \cos\alpha>0 | ||
| \displaystyle \alpha=\frac{\pi}{2} | \displaystyle \sin\alpha=1 | \displaystyle \cos\alpha=0 | ||
| \displaystyle \frac{\pi}{2}<\alpha<\pi | \displaystyle \sin\alpha>0 | \displaystyle \cos\alpha<1 | ||
| \displaystyle \alpha=\pi | \displaystyle \sin\alpha=0 | \displaystyle \cos\alpha=-1 | ||
| \displaystyle \pi<\alpha<\frac{3\pi}{2} | \displaystyle \sin\alpha<0 | \displaystyle \cos\alpha<1 | ||
| \displaystyle \alpha=\frac{3\pi}{2} | \displaystyle \sin\alpha=1 | \displaystyle \cos\alpha=0 | ||
| \displaystyle \frac{3\pi}{2}<\alpha<2\pi | \displaystyle \sin\alpha<0 | \displaystyle \cos\alpha>1 | ||
| \displaystyle \alpha=2\pi=0 |
Vi ser då att
\displaystyle a_x=a_xe_x=a\cos\alpha e_x
\displaystyle a_y=a_ye_y=a\sin\alpha e_y
Komposanten \displaystyle a_x kan således uttryckas med hjälp av komponenten \displaystyle a_x. Motsvarande gäller för komposanten \displaystyle a_y.
När enhetsvektorn \displaystyle e_x används för att bilda en komposant brukar kallas basvektor. Motsvarande gäller för basvektorn \displaystyle e_y.
Vi kan alltså skriva vektorn \displaystyle a med hjälp av basvektorerna \displaystyle e_x och \displaystyle e_y:
\displaystyle a=a_x+a_y=a_xe_x+a_ye_y=a\cos\alpha e_x+a\sin\alpha e_y
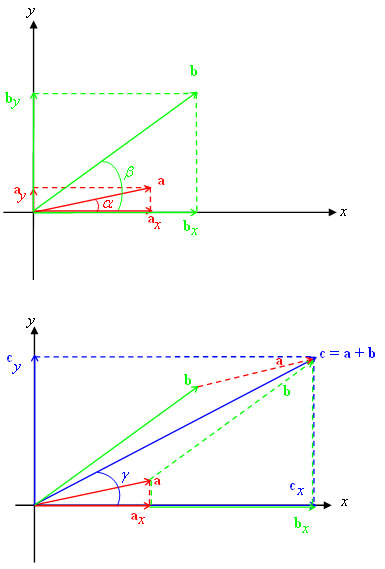
Om vi alltid räknar vinkeln positiv moturs från x-axeln hamnar den i vårt fall för vektorn \displaystyle b så att sinus för vinkeln blir < 0 medan cosinus för vinkeln > 0.
\displaystyle b=b_x+b_y=b_xe_x+b_ye_y=b\cos\beta e_x+b\sin\beta e_y
Således får vi
\displaystyle c=c_x+c_y=c_xe_x+c_ye_y=c\cos\gamma e_x+c\sin\gamma e_y =
\displaystyle =a_xe_x+a_ye_y+b_xe_x+b_ye_y=a_xe_x+b_xe_x+a_ye_y+b_ye_y=
\displaystyle =(a_x+b_x)e_x+(a_y+b_y)e_y=(a\cos\alpha + b\cos\beta)e_x+(a\sin\alpha +b\sin\beta)e_y
Således är
\displaystyle c=c_x+c_y=(a_x+b_x)+(a_y+b_y)
| \displaystyle c_x=a_x+b_x | \displaystyle c_y=a_y+b_y | |
| \displaystyle c\cos\gamma =a\cos\alpha + b\cos\beta | \displaystyle c\sin\gamma =a\sin\alpha + b\sin\beta |
I stället för att skriva ut a med basvektorerna a=axex+ayey eller a=acosËex+asinËey så skriver man kortare a=(ax;ay) eller a=(acosË;asinË) med kommatecken mellan komponenterna.
Vid heltal har man inga problem med denna notation: a=(5;7)m=s2 men vid decimaltal byter man ut kommatecknet mot semikolon: a=(4;2;3;8)m=s2
Nollvektorn
Nollvektorn 0=(0;0) har längden 0. Den är den enda vektor som saknar riktning.