2.4 Kraftmoment
FörberedandeFysik
| Rad 27: | Rad 27: | ||
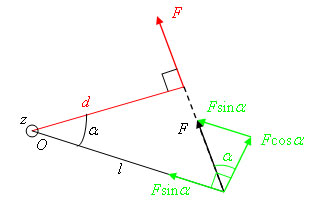
Samma kraft kan ha olika <i>vridande förmåga</i> eller <i>kraftmoment</i> beroende på längden av <i>hävarmen</i>, som är det vinkelräta avståndet från <i>momentpunkten</i>, som ligger på vridningsaxeln, fram till kraftens verkningslinje (den åt båda hållen förlängda linje som kan dras längs kraftens riktning). | Samma kraft kan ha olika <i>vridande förmåga</i> eller <i>kraftmoment</i> beroende på längden av <i>hävarmen</i>, som är det vinkelräta avståndet från <i>momentpunkten</i>, som ligger på vridningsaxeln, fram till kraftens verkningslinje (den åt båda hållen förlängda linje som kan dras längs kraftens riktning). | ||
| - | |||
[[Bild:havstang.jpg|center]] | [[Bild:havstang.jpg|center]] | ||
| + | |||
Om F är vinkelrät mot d (om vi betraktar dessa som vektorer, fast vektoregenskapen inte angivits i figuren) och de båda ligger i xy-planet (skärmens plan), så är kraftmomentet med avseende på punkten O : | Om F är vinkelrät mot d (om vi betraktar dessa som vektorer, fast vektoregenskapen inte angivits i figuren) och de båda ligger i xy-planet (skärmens plan), så är kraftmomentet med avseende på punkten O : | ||
Versionen från 14 december 2009 kl. 09.55
| Teori | Övningar |
Mål och innehåll
Innehåll
- Kraftmoment
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Definiera begreppet kraftmoment.
- Redogöra för den fysikaliska innebörden av kraftmoment som ett uttryck för en krafts vridande förmåga.
- Skilja mellan riktningen av kraftmomentet som uttryck för vridande förmåga åt olika håll.
- Förklara varför man vill uttrycka kraftmoment som en vektor.
- Ställa upp och räkna ut kraftmoment som hävarm * kraft.
- Beskriva vad som händer med kraftmomentet om man flyttar kraften längs sin verkningslinje.
Samma kraft kan ha olika vridande förmåga eller kraftmoment beroende på längden av hävarmen, som är det vinkelräta avståndet från momentpunkten, som ligger på vridningsaxeln, fram till kraftens verkningslinje (den åt båda hållen förlängda linje som kan dras längs kraftens riktning).
Om F är vinkelrät mot d (om vi betraktar dessa som vektorer, fast vektoregenskapen inte angivits i figuren) och de båda ligger i xy-planet (skärmens plan), så är kraftmomentet med avseende på punkten O :
MO=dFez
där z-axeln och MO går ut från skärmens plan mot dina ögon.
Observera att om kraften F förflyttas längs sin verkningslinje, så att den inte angriper i en punkt som ligger så att kraften blir vinkelrät mot förbindelselinjen fram till O , så förändras inte kraftmomentet, ty man måste ta den vinkelräta projektionen:
MO=FlcosËez=Fdez=FcosËlez
eftersom FsinË saknar hävarm fram till O.
Skulle kraften F vara riktad åt motsatt håll
så får MO motsatt riktning: MO=ÀdFez , där z-axeln alltjämt går ut från skärmens plan mot dina ögon medan MO går in i skärmen bort från dina ögon.