3.3 Kraftekvationen
FörberedandeFysik
| (8 mellanliggande versioner visas inte.) | |||
| Rad 26: | Rad 26: | ||
:* Ställa upp och räkna ut vilka krafter som verkar på en partikel i rörelse och därmed kunna bestämma partikelns acceleration. | :* Ställa upp och räkna ut vilka krafter som verkar på en partikel i rörelse och därmed kunna bestämma partikelns acceleration. | ||
</div> | </div> | ||
| + | |||
| + | FÖRFATTARE: Ian Cohen, KTH Mekanik | ||
| + | |||
=Kraftekvationen - Newtons andra lag= | =Kraftekvationen - Newtons andra lag= | ||
| Rad 31: | Rad 34: | ||
Här behandlas endast rätlinjig rörelse. | Här behandlas endast rätlinjig rörelse. | ||
| - | Enligt Newtons teori gäller att om en partikel med massa <math>m</math> har en acceleration | + | Enligt Newtons teori gäller att om en partikel med massa <math>m</math> har en acceleration <math>\textbf{a}</math> , måste en kraft <math>\textbf{F}</math> verka på partikeln enligt |
| - | + | <math>\textbf{F}=m\cdot \textbf{a}</math> | |
| - | Detta samband mellan kraft, massa och acceleration kallas Newtons andra lag, eller kraftekvationen, där | + | Detta samband mellan kraft, massa och acceleration kallas Newtons andra lag, eller kraftekvationen, där <math>\textbf{a}</math> är momentanaccelerationen. |
| - | Omvänt kan man konstatera att om en kraft | + | Omvänt kan man konstatera att om en kraft <math>\textbf{F}</math> verkar på en partikel med massa <math>m</math> kommer partikeln att få en acceleration <math>\textbf{a}</math> enligt |
| - | + | <math>\textbf{a}=\frac{\textbf{F}}{m}</math> | |
Om kraftens storlek är <math>F</math> och accelerationens storlek är <math>a</math> fås <math>a=\frac{F}{m}</math>. | Om kraftens storlek är <math>F</math> och accelerationens storlek är <math>a</math> fås <math>a=\frac{F}{m}</math>. | ||
| Rad 60: | Rad 63: | ||
Exempel: | Exempel: | ||
| + | [[Bild:kraft_1.jpg|center]] | ||
| + | Här har '''F'''<math>_1</math> storleken <math>5N</math> och '''F'''<math>_2</math> storleken <math>3N</math>. Då är kraftsumman <math>2N</math> till vänster, dvs kraftsumman pekar i den negativa riktningen. | ||
| - | + | Vi får <math>-2N=ma</math>. | |
| - | Vi får À2N=ma . | ||
Om krafterna däremot inte ligger längs en och samma rät linje måste vi använda vektoralgebra för att bestämma krafternas resultant: | Om krafterna däremot inte ligger längs en och samma rät linje måste vi använda vektoralgebra för att bestämma krafternas resultant: | ||
| + | [[Bild:kraft_2.jpg|center]] | ||
| + | Här verkar '''F'''<math>_1</math> och '''F'''<math>_2</math> på partikeln. Vi bestämmer deras resultant '''R''' och tillämpar kraftekvationen med '''R''' som kraftsumma. Det betyder att partikeln har en acceleration i '''R''' :s riktning och en storlek <math>\frac{R}{m}</math>. | ||
| - | |||
| - | Här verkar F1 och F2 på partikeln. Vi bestämmer deras resultant R och tillämpar kraftekvationen med R som kraftsumma. Det betyder att partikeln har en acceleration i R :s riktning och en storlek Rm. | ||
Det omvända gäller också: | Det omvända gäller också: | ||
| - | R | + | '''R''' verkar på en partikel. Vi delar upp '''R''' i komposanter '''F'''<math>_1</math> och '''F'''<math>_2</math>. Då har partikeln en acceleration <math>\frac{\textbf{F}_1}{m}</math> i '''F'''<math>_1</math>:s riktning och en acceleration <math>\frac{\textbf{F}_2}{m}</math> i '''F'''<math>_2</math>:s riktning. |
<div class="inforuta" style="width: 580px"> | <div class="inforuta" style="width: 580px"> | ||
===Råd för inläsning=== | ===Råd för inläsning=== | ||
| + | |||
====Lästips==== | ====Lästips==== | ||
| - | :'''Läs''' i HEUREKA! Fysik kurs | + | :'''Läs''' i ''HEUREKA! Fysik kurs 1'' kapitel 11, avsnitten 4-8. |
====Länktips==== | ====Länktips==== | ||
| - | + | :[https://science.howstuffworks.com/innovation/scientific-experiments/newton-law-of-motion3.htm Läs mer om Newtons andra lag här]</div> | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | :[ | + | |
Nuvarande version
| Teori | Övningar |
Mål och innehåll
Innehåll
- Kraftekvationen - Newtons andra lag
- Kraftekvationen då flera krafter verkar
Läromål
Efter detta avsnitt ska du ha lärt dig att:
- Redogöra för innebörden i Newton andra lag.
- Skilja mellan mellan Newtons ekvation i vektorform och skalärform.
- Inse att om en partikel har en acceleration så verkar det en kraft på den.
- Beskriva vad som händer om en kraft verkar på en partikel i rörelse.
- Beskriva vad som händer om flera krafter verkar på en partikel i rörelse.
- Ställa upp och räkna ut accelerationen hos en partikel och därmed kunna bestämma vilka krafter som verkar på partikeln i rörelse.
- Ställa upp och räkna ut vilka krafter som verkar på en partikel i rörelse och därmed kunna bestämma partikelns acceleration.
FÖRFATTARE: Ian Cohen, KTH Mekanik
Kraftekvationen - Newtons andra lag
Här behandlas endast rätlinjig rörelse.
Enligt Newtons teori gäller att om en partikel med massa
a
Detta samband mellan kraft, massa och acceleration kallas Newtons andra lag, eller kraftekvationen, där
Omvänt kan man konstatera att om en kraft
Om kraftens storlek är
En Newton (1 N) är enheten för kraftstorheten och definieras som den kraft som ger en acceleration på 
s2
Vi har tidigare konstaterat att tyngdaccelerationen nära jorden är 
82ms2
En kropp som faller fritt nära jorden har en tyngdkraft
Kraftekvationen då flera krafter verkar
En kropp kan utsättas för flera krafter. I så fall skall man använda deras kraftsumma i kraftekvationen.
Kraftsumma = massa
Detta är ganska enkelt om krafterna verkar längs en och samma rät linje. Man måste välja en positiv riktning och alla krafter med motsatt riktning är negativa.
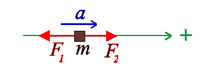
Exempel:
Här har F\displaystyle _1 storleken \displaystyle 5N och F\displaystyle _2 storleken \displaystyle 3N. Då är kraftsumman \displaystyle 2N till vänster, dvs kraftsumman pekar i den negativa riktningen.
Vi får \displaystyle -2N=ma.
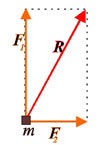
Om krafterna däremot inte ligger längs en och samma rät linje måste vi använda vektoralgebra för att bestämma krafternas resultant:
Här verkar F\displaystyle _1 och F\displaystyle _2 på partikeln. Vi bestämmer deras resultant R och tillämpar kraftekvationen med R som kraftsumma. Det betyder att partikeln har en acceleration i R :s riktning och en storlek \displaystyle \frac{R}{m}.
Det omvända gäller också:
R verkar på en partikel. Vi delar upp R i komposanter F\displaystyle _1 och F\displaystyle _2. Då har partikeln en acceleration \displaystyle \frac{\textbf{F}_1}{m} i F\displaystyle _1:s riktning och en acceleration \displaystyle \frac{\textbf{F}_2}{m} i F\displaystyle _2:s riktning.
