Lösning 2.6:7
FörberedandeFysik
(Skillnad mellan versioner)
(Ny sida: Kraftmomentet med avseende på <math>O</math> är noll. <math>T\sin45^\circ a–Mga–mg2a=0</math><br\> <math>T/ \sqrt{2}–Mg–2mg=0</math><br\> <math>T=(M+2m)g/ \sqrt{2}</math>) |
|||
| Rad 1: | Rad 1: | ||
| - | + | Vi frilägger bommen och ritar ut de krafter som verkar. | |
| - | <math> | + | [[Bild:Svar_2_6_7.jpg]] |
| - | <math>T/ \sqrt{2} | + | |
| - | <math>T= | + | |
| + | <math> \sin{45^\textrm{o}}=\frac{1}{\sqrt{2}} </math> | ||
| + | Vi sätter upp momentekvationen kring punkten <math>O</math> | ||
| + | Posiva moment medurs ger moment kring <math>{O} : M_{O}=\sum_{i}F_{i}d_{i}</math> | ||
| + | |||
| + | Vi vet också att bommen inte roterar, alltså gäller att | ||
| + | |||
| + | <math>M_{O}=0</math> | ||
| + | |||
| + | <math>M_{O}=-\frac{T}{\sqrt{2}}\cdot a+Mg\cdot a+mg\cdot 2a</math> | ||
| + | |||
| + | Vi sätter ihop våra båda ekvationer och får | ||
| + | |||
| + | <math>-\frac{T}{\sqrt{2}}\cdot a+Mg\cdot a+mg\cdot 2a=0</math> | ||
| + | |||
| + | <math>\Rightarrow -\frac{T}{\sqrt{2}}+Mg+2mg=0 | ||
| + | </math> | ||
| + | |||
| + | <math>\Rightarrow T =\sqrt{2}g(M + 2m)</math> | ||
Nuvarande version
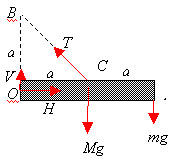
Vi frilägger bommen och ritar ut de krafter som verkar.
\displaystyle \sin{45^\textrm{o}}=\frac{1}{\sqrt{2}}
Vi sätter upp momentekvationen kring punkten \displaystyle O
Posiva moment medurs ger moment kring \displaystyle {O} : M_{O}=\sum_{i}F_{i}d_{i}
Vi vet också att bommen inte roterar, alltså gäller att
\displaystyle M_{O}=0
\displaystyle M_{O}=-\frac{T}{\sqrt{2}}\cdot a+Mg\cdot a+mg\cdot 2a
Vi sätter ihop våra båda ekvationer och får
\displaystyle -\frac{T}{\sqrt{2}}\cdot a+Mg\cdot a+mg\cdot 2a=0
\displaystyle \Rightarrow -\frac{T}{\sqrt{2}}+Mg+2mg=0
\displaystyle \Rightarrow T =\sqrt{2}g(M + 2m)