FörberedandeFysik

Teori

Övningar

Arbete

Inom fysiken vill man definiera arbete på ett sätt som liknar betydelsen av begreppet man möter i vardagslivet.

Det fysikaliska begreppet arbete behövs för att utvidga Newtons teori.

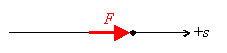
Antag att en kraft eller en resultant F av ett antal krafter verkar på en partikel.

Här betraktar vi endast konstant F och rörelse längs en rät linje som har positiv riktning.

Antag ytterligare att partikeln förflyttas med \displaystyle s som kan vara positiv eller negativ:

Då säger vi att kraften eller resultanten med storleken \displaystyle F har uträttat ett arbete \displaystyle W av storleken:

\displaystyle W=Fs

Om t.ex. \displaystyle F=3 N och \displaystyle s=-6m, har kraften uträttat arbetet \displaystyle W=-18Nm=-18J. Enheten Nm kallas joule (J). Det rekommenderas att använda joule (J) som enhet för arbete eftersom Nm används för en helt annan storhet, nämligen kraftmoment.

Arbetet som definieras här som en produkt av kraft och förflyttning sammanfaller någorlunda med hur vi uppfattar arbetet i vardagslivet: Ju större kraft och förflyttning desto större arbete.

Arbete kan vara negativt. Både kraft och sträcka anges med riktning och det innebär att produkten av dessa också har en 'riktning', den kan vara antingen negativ eller positiv och betecknar snarare vilket håll arbetet utförs åt än att arbetet som utförs ska ses som ett energitillskott.

Vi har ännu inte nämnt någonting om partikelns hastighet. Den kommer i bilden när vi definierar den besläktade storheten energi, närmare bestämt:

Kinetisk energi

Energi kan betraktas som en källa ur vilken krafter kan uträtta arbete: En kraft med storleken \displaystyle F som uträttar ett arbete på en kropp, ändrar kroppens energi dvs:

Arbete = energiändring

förutsatt att arbetet inte är noll. Detta är ett sätt att införa begreppet energi.

Mest grundläggande är kinetisk energi, även kallad rörelseenergi. Kinetisk energi härrör ur en kropps rörelse. Om partikeln har en massa \displaystyle m och en hastighet \displaystyle v definieras partikelns kinetiska eller rörelseenergi \displaystyle E_k som:

\displaystyle E_k=\frac{1}{2}mv^2

Anta t.ex. att en partikel med massan \displaystyle m släpps utan hastighet från en höjd. På partikeln verkar tyngdkraften \displaystyle F=mg. Efter att partikeln har fallit en viss höjd \displaystyle h har tyngdkraften \displaystyle F uträttat arbetet \displaystyle mgh. Partikelns hastighet är \displaystyle v och dess kinetiska energi \displaystyle \frac{1}{2}mv^2.

Partikelns kinetiska energi har då ökat med \displaystyle \frac{1}{2}mv^2 eftersom hastigheten var noll i början. Så får vi arbetet som ändringen av den kinetiska energin:

\displaystyle mgh=\frac{1}{2}mv^2

Potentiell energi

Om däremot samma partikel vilar på marken och vi lyfter den till en höjd \displaystyle h behövs det en kraft \displaystyle F=mg för att övervinna tyngdkraften. Arbetet som denna kraft har uträttat är enligt arbetets definition, kraft gånger förflyttning dvs: \displaystyle mgh.

Då partikelns hastighet är noll i slutet, är även ändringen av den kinetiska energin noll.

Men kraften \displaystyle F som lyft partikeln har uträttat arbete. Därmed måste enligt definitionen ovan en ändring av energin förekommit dvs partikeln måste ha fått energi, eftersom partikeln befinner sig nu på en högre höjd \displaystyle h än tidigare. Den här andra sortens energi definieras som potentiell energi \displaystyle E_p, även kallad lägesenergi:

\displaystyle E_p=mgh

Vi kan släppa partikeln så att den börjar falla varvid parikelns potentiella energi successivt omvandlas till kinetisk energi. Potentiell energi är en form av energi som är så att säga lagrad i partikeln och kan omvandlas till den andra formen, den kinetiska energin. När partikeln efter ett tag nått marken är hela dess potentiella energi förbrukad dvs omvandlad till kinetisk energi.

Vi kan sammanfatta så här:

En liten boll med massan \displaystyle m ligger på marken. Den har noll potentiell och noll kinetisk energi.

En kraft lyfter bollen till en höjd \displaystyle h och uträttar ett arbete \displaystyle mgh. Då har bollen en potentiell energi \displaystyle mgh och en kinetisk energi noll. Bollen släpps och då den når marken har den en potentiell energi noll men en kinetisk energi på \displaystyle \frac{1}{2}mv^2 som är lika med \displaystyle mgh.

Under uppåtfasen har källan till kraften som lyfter bollen förbrukat lika mycket energi \displaystyle mgh. Denna källa kan t.ex. vara kemisk energi, t.ex. om det är en person som har hissat upp bollen.

Energiprincipen

I exemplet med bollen släpper man bollen från en viss höjd \displaystyle h. Vid detta ögonblick är den potentiella energin maximal och den kinetiska noll. Under rörelsen omvandlas den potentiella energin successivt till kinetisk energi tills bollen når marken. Vid ögonblicket före islaget på marken är den kinetiska energin maximal och den potentiella noll. Men innan, under själva rörelsen är bollens energi en blandning av kinetisk och potentiell energi.

Bildar man summan av kinetisk och potentiell energi kan man visa att den under hela rörelsen är konstant och lika med \displaystyle mgh. Om man bortser från andra krafter som ev. också uträttar arbete, t.ex. luftmotstånd, friktion eller vind, kan man säga att summan av kinetisk och potentiell energi är konstant vilket kallas energiprincipen: Bollens totala energi \displaystyle E_{total} är alltid konstant:

\displaystyle E_{total}=E_k+E_p= const

Denna princip bygger på att en krafts arbete på en partikel ändrar partikelns energi. Om arbetet är noll är energiändringen noll.

Om vi kastar upp bollen vertikalt med hastigheten \displaystyle v, då når den upp till en viss höjd \displaystyle h, och vi har \displaystyle mgh=\frac{1}{2}mv^2, vilket kan förenklas till \displaystyle gh=\frac{1}{2}v^2 och innebär att energiprincipen är oberoende av partikelns massa dvs gäller generellt för alla partiklar.

Eftersom endast ändringen av energi dvs energiskillnaden är av betydelse, kan man välja vilken höjd som helst som nivån där energin är noll. Detta läge kallas för nollnivå. Det måste alltså inte vara marken.

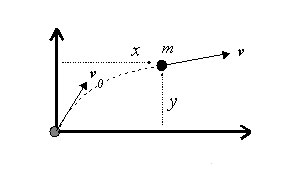
Principen är universell och fungerar lika bra även för en bana i två dimensioner, t.ex. vid kaströrelse. Här kan kastets utgångspunkt väljas som nollnivå:

Om v0 är bollens begynnelsehastighet (ett konstant värde) och v hastigheten under hela kaströrelsen, är bollens totala energi Ek+Ep konstant:

21mv02+0=21mv2+mgy

där till vänster om likheten står bollens totala energi vid kastets utgångspunkt (konstant pga konstant begynnelsehastighet) och till höger den totala energin under hela kaströrelsen, i båda fall som summan av kinetisk och potentiell enegi.

Annat exempel: En boll rullar på en glatt bana

Om vi betraktar två situationer av den rullande bollen som visas på bilden, ger energiprincipen 21mv12+mgh1=21mv22+mgh2 eller efter att ha eliminerat m

21v12+gh1=21v22+gh2

Energi mäts med samma enhet som arbete pga arbete = energiändring, vilket innebär att enheten är joule (J).

Effekt

En maskin genererar en kraft F som uträttar ett arbete W . Hur lång tid t tar det att uträtta detta arbete? Frågan kan vara av praktiskt intresse då maskinen inte orkar jobba hur snabbt som helst. Vi behöver en storhet som involverar tiden. Så kommer begreppet effekt i bilden.

Ursprungligen definieras effekt som P=tidarbete. Men pga arbete = energiändring skrivs effekt ofta som

P=tidenergi

som ger upphov till enheten joule per sekund, även kallad watt (W): 1 W = 1 J/sec. Ibland används även en hästkraft som är 0,735 kW.

Råd för inläsning