2.3 Andragradsuttryck
Sommarmatte 1
| Versionen från 14 maj 2007 kl. 11.05 (redigera) Lina (Diskussion | bidrag) (→Parabler) ← Gå till föregående ändring |
Nuvarande version (6 juli 2007 kl. 06.37) (redigera) (ogör) KTH.SE:u1tyze7e (Diskussion | bidrag) m |
||
| (18 mellanliggande versioner visas inte.) | |||
| Rad 97: | Rad 97: | ||
| *$x+1 =\sqrt{9} = 3\,$ och därmed $\,x=-1+3=2\,$, | *$x+1 =\sqrt{9} = 3\,$ och därmed $\,x=-1+3=2\,$, | ||
| *$x+1 =-\sqrt{9} = -3\,$ och därmed $\,x=-1-3=-4\,$. <br><br> | *$x+1 =-\sqrt{9} = -3\,$ och därmed $\,x=-1-3=-4\,$. <br><br> | ||
| - | <li>Lös ekvationen $\ 2x^2 -2x - \frac{2}{3} = 0\,$. <br><br> | + | <li>Lös ekvationen $\ 2x^2 -2x - \frac{3}{2} = 0\,$. <br><br> |
| Dividera båda led med 2 | Dividera båda led med 2 | ||
| $$x^2-x-\textstyle\frac{3}{4}=0\mbox{.}$$ | $$x^2-x-\textstyle\frac{3}{4}=0\mbox{.}$$ | ||
| Rad 154: | Rad 154: | ||
| Grafen till en andragradsfunktion kallas för en parabel och figurerna visar utseendet för två typexempel $\,y=x^2\,$ och $\,y=-x^2$. | Grafen till en andragradsfunktion kallas för en parabel och figurerna visar utseendet för två typexempel $\,y=x^2\,$ och $\,y=-x^2$. | ||
| - | [[Bild:t_3_1_1b.gif]] [[Bild:t_3_1_2b.gif]] | + | <center>[[Bild:t_3_1_1b.gif]] [[Bild:t_3_1_2b.gif]]</center> |
| Eftersom uttrycket $\,x^2\,$ är som minst när $\,x=0\,$ har parabeln $\,y=x^2\,$ ett minimum när $\,x=0\,$ och parabeln $\,y=-x^2\,$ ett maximum för $\,x=0\,$. | Eftersom uttrycket $\,x^2\,$ är som minst när $\,x=0\,$ har parabeln $\,y=x^2\,$ ett minimum när $\,x=0\,$ och parabeln $\,y=-x^2\,$ ett maximum för $\,x=0\,$. | ||
| Rad 162: | Rad 162: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 5''' | '''Exempel 5''' | ||
| + | [[Bild:t_3_1_3b.gif|right]] | ||
| <ol type="a"> | <ol type="a"> | ||
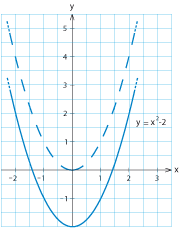
| <li>Skissera parabeln $\ y=x^2-2\,$. <br><br> | <li>Skissera parabeln $\ y=x^2-2\,$. <br><br> | ||
| - | Jämfört med parabeln $\,y=x^2\,$ har punkter på parabeln $\,y=x^2-2\,$ $y$-värden som är två enheter mindre, d.v.s. parabeln är förskjuten två enheter neråt i $y$-led. <br><br> | + | Jämfört med parabeln $\,y=x^2\,$ har punkter på parabeln ($\,y=x^2-2\,$) $y$-värden som är två enheter mindre, d.v.s. parabeln är förskjuten två enheter neråt i $y$-led. <br><br> |
| + | </ol> | ||
| + | |||
| + | <br><br><br><br><br><br><br> | ||
| + | |||
| + | [[Bild:t_3_1_4b.gif|right]] | ||
| + | <ol type="a" start=2> | ||
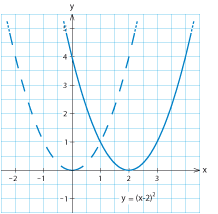
| <li>Skissera parabeln $\ y=(x-2)^2\,$. <br><br> | <li>Skissera parabeln $\ y=(x-2)^2\,$. <br><br> | ||
| På parabeln $\,y=(x-2)^2\,$ behöver vi välja $x$-värden två enheter större jämfört med parabeln $\,y=x^2\,$ för att få motsvarande $y$-värden. Alltså är parabeln $\,y=(x-2)^2\,$ förskjuten två enheter åt höger jämfört med $\,y=x^2\,$.<br><br> | På parabeln $\,y=(x-2)^2\,$ behöver vi välja $x$-värden två enheter större jämfört med parabeln $\,y=x^2\,$ för att få motsvarande $y$-värden. Alltså är parabeln $\,y=(x-2)^2\,$ förskjuten två enheter åt höger jämfört med $\,y=x^2\,$.<br><br> | ||
| + | </ol> | ||
| + | |||
| + | <br><br><br><br><br><br><br><br> | ||
| + | |||
| + | [[Bild:766663.gif|right]] | ||
| + | <ol type="a" start=3> | ||
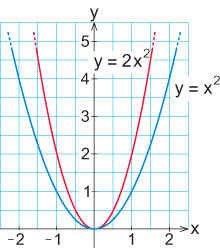
| <li>Skissera parabeln $\,y=2x^2\,$. <br><br> | <li>Skissera parabeln $\,y=2x^2\,$. <br><br> | ||
| Varje punkt på parabeln $\,y=2x^2\,$ har dubbelt så stort $y$-värde än vad motsvarande punkt med samma $x$-värde har på parabeln $\,y=x^2\,$. Parabeln $\,y=2x^2\,$ är expanderad med faktorn $2$ i $y$-led jämfört med $\,y=x^2\,$. | Varje punkt på parabeln $\,y=2x^2\,$ har dubbelt så stort $y$-värde än vad motsvarande punkt med samma $x$-värde har på parabeln $\,y=x^2\,$. Parabeln $\,y=2x^2\,$ är expanderad med faktorn $2$ i $y$-led jämfört med $\,y=x^2\,$. | ||
| </ol> | </ol> | ||
| - | {| width="100%" border="0" | + | <br><br><br><br><br><br><br><br> |
| - | |- | + | |
| - | |width="33%" | [[Bild:t_3_1_3b.gif]] | + | |
| - | |width="33%" | [[Bild:t_3_1_4b.gif]] | + | |
| - | |width="33%" | [[Bild:766663.gif]] | + | |
| - | |- | + | |
| - | |width="33%" align="center"|Grafen till $\,y=x^2-2$ | + | |
| - | |width="33%" align="center"|Grafen till $\,y=(x-2)^2$ | + | |
| - | |width="33%" align="center"|Grafen till $\,y=2x^2$ | + | |
| - | |} | + | |
| </div> | </div> | ||
| Rad 188: | Rad 195: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 6''' | '''Exempel 6''' | ||
| + | [[Bild:t_3_1_5b.gif|right]] | ||
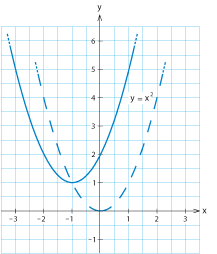
| Skissera parabeln $\ y=x^2+2x+2\,$. | Skissera parabeln $\ y=x^2+2x+2\,$. | ||
| Rad 196: | Rad 204: | ||
| så ser vi från det resulterande uttrycket $\,y= (x+1)^2+1\,$ att parabeln är förskjuten en enhet åt vänster i $x$-led jämfört med $\,y=x^2\,$ (eftersom det står $\,(x+1)^2\,$ istället för $\,x^2\,$) och en enhet uppåt i $y$-led. | så ser vi från det resulterande uttrycket $\,y= (x+1)^2+1\,$ att parabeln är förskjuten en enhet åt vänster i $x$-led jämfört med $\,y=x^2\,$ (eftersom det står $\,(x+1)^2\,$ istället för $\,x^2\,$) och en enhet uppåt i $y$-led. | ||
| - | [[Bild:t_3_1_5b.gif]]<br><br> | + | <br><br><br><br><br><br> |
| </div> | </div> | ||
| Rad 208: | Rad 216: | ||
| En punkt ligger på $x$-axeln om dess $y$-koordinat är noll, och de punkter på parabeln som har $y=0$ har en $x$-koordinat som uppfyller ekvationen | En punkt ligger på $x$-axeln om dess $y$-koordinat är noll, och de punkter på parabeln som har $y=0$ har en $x$-koordinat som uppfyller ekvationen | ||
| $$x^2-4x+3=0\mbox{.}$$ | $$x^2-4x+3=0\mbox{.}$$ | ||
| + | [[Bild:t_3_1_6b.gif|right]] | ||
| Vänsterledet kvadratkompletteras | Vänsterledet kvadratkompletteras | ||
| $$x^2-4x+3=(x-2)^2-2^2+3=(x-2)^2-1$$ | $$x^2-4x+3=(x-2)^2-2^2+3=(x-2)^2-1$$ | ||
| Rad 218: | Rad 227: | ||
| Parabeln skär $x$-axeln i punkterna $\,(1,0)\,$ och $\,(3,0)\,$. | Parabeln skär $x$-axeln i punkterna $\,(1,0)\,$ och $\,(3,0)\,$. | ||
| - | [[Bild:t_3_1_6b.gif]]<br><br> | + | <br><br> |
| </div> | </div> | ||
| Rad 224: | Rad 233: | ||
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 8''' | '''Exempel 8''' | ||
| - | + | [[Bild:t_3_1_7b.gif|right]] | |
| Bestäm det minsta värde som uttrycket $\,x^2+8x+19\,$ antar. | Bestäm det minsta värde som uttrycket $\,x^2+8x+19\,$ antar. | ||
| <br> | <br> | ||
| Rad 234: | Rad 243: | ||
| I figuren till höger ser vi att hela parabeln $\,y=x^2+8x+19\,$ ligger ovanför $x$-axeln och har ett minimumvärde 3 när $\,x=-4\,$. | I figuren till höger ser vi att hela parabeln $\,y=x^2+8x+19\,$ ligger ovanför $x$-axeln och har ett minimumvärde 3 när $\,x=-4\,$. | ||
| - | [[Bild:t_3_1_7b.gif]]<br><br> | + | <br><br> |
| </div> | </div> | ||
| Rad 243: | Rad 252: | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| '''Råd för inläsning''' | '''Råd för inläsning''' | ||
| + | |||
| + | '''Grund- och slutprov''' | ||
| + | |||
| + | Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge. | ||
| + | |||
| '''Tänk på att:''' | '''Tänk på att:''' | ||
| Rad 264: | Rad 278: | ||
| </div> | </div> | ||
| - | |||
| - | |||
| - | <small>© Copyright 2007, math.se</small> | ||
| - | |||
| - | |||
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
|
[redigera] Teori[redigera] AndragradsekvationerEn andragradsekvation är en ekvation som kan skrivas som $$x^2+px+q=0$$ där $x$ är den obekanta och $p$ och $q$ är konstanter.
Ekvationen $\,x^2=a\,$ där $a$ är ett postivt tal har två lösningar (rötter) $\,x=\sqrt{a}\,$ och $\,x=-\sqrt{a}\,$. Exempel 1
Exempel 2
För att lösa allmänna andragradsekvationer använder vi en teknik som kallas kvadratkomplettering. Om vi betraktar kvadreringsregeln $$x^2 + 2ax + a^2 = (x+a)^2$$ och subtraherar $a^2$ från båda led så får vi Kvadratkomplettering: $$x^2 +2ax = (x+a)^2 -a^2$$ Exempel 3
Tips: Tänk på att man alltid kan pröva lösningar till en ekvation genom att sätta in värdet och se om ekvationen blir uppfylld. Man gör detta för att upptäcka eventuella slarvfel. För exempel 3a ovan har vi två fall att pröva. Vi kallar vänster- och högerleden för VL respektive HL:
I båda fallen kommer vi fram till VL = HL. Ekvationen är alltså uppfylld i båda fallen. Med kvadratkomplettering går det att visa att den allmänna andragradsekvationen $$x^2+px+q=0$$ har lösningarna $$x = - \displaystyle\frac{p}{2} \pm \sqrt{\left(\frac{p}{2}\right)^2-q}$$ förutsatt att uttrycket under rottecknet inte är negativt. Ibland kan man faktorisera ekvationer och direkt se vilka lösningarna är. Exempel 4
[redigera] ParablerFunktionerna $$\eqalign{y&=x^2-2x+5\cr y&=4-3x^2\cr y&=\textstyle\frac{1}{5}x^2 +3x}$$ är exempel på andragradsfunktioner. Allmänt kan en andragradsfunktion skrivas som $$y=ax^2+bx+c$$ där $a$, $b$ och $c$ är konstanter och där $a\ne0$. Grafen till en andragradsfunktion kallas för en parabel och figurerna visar utseendet för två typexempel $\,y=x^2\,$ och $\,y=-x^2$. 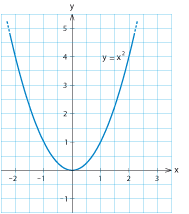 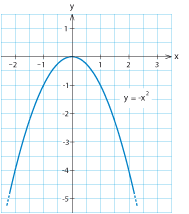 Eftersom uttrycket $\,x^2\,$ är som minst när $\,x=0\,$ har parabeln $\,y=x^2\,$ ett minimum när $\,x=0\,$ och parabeln $\,y=-x^2\,$ ett maximum för $\,x=0\,$. Notera också att parablerna ovan är symmetriska kring $y$-axeln eftersom värdet på $\,x^2\,$ inte beror på vilket tecken $x$ har. Exempel 5
Med kvadratkomplettering kan vi behandla alla typer av parabler. Exempel 6 Skissera parabeln $\ y=x^2+2x+2\,$.
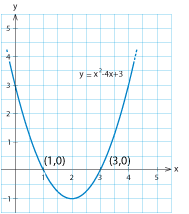
Exempel 7 Bestäm var parabeln $\,y=x^2-4x+3\,$ skär $x$-axeln.
Vänsterledet kvadratkompletteras $$x^2-4x+3=(x-2)^2-2^2+3=(x-2)^2-1$$ och detta ger ekvationen $$(x-2)^2= 1 \; \mbox{.}$$ Efter rotutdragning får vi lösningarna
Parabeln skär $x$-axeln i punkterna $\,(1,0)\,$ och $\,(3,0)\,$.
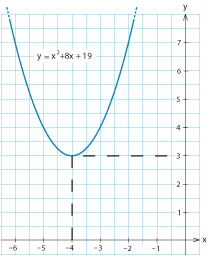
Exempel 8 Bestäm det minsta värde som uttrycket $\,x^2+8x+19\,$ antar.
I figuren till höger ser vi att hela parabeln $\,y=x^2+8x+19\,$ ligger ovanför $x$-axeln och har ett minimumvärde 3 när $\,x=-4\,$.
Råd för inläsning Grund- och slutprov Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge.
Lägg ner mycket tid på algebra! Algebra är matematikens alfabet. När du väl har förstått algebra, kommer din förståelse av statistik, yta, volym och geometri vara mycket större.
för dig som vill fördjupa dig ytterligare eller skulle vilja ha en längre förklaring Läs mer om andragradsekvationer på engelska Wikipedia Läs mer om andragradsekvationer i MathWorld 101 uses of a quadratic equation - by Chris Budd and Chris Sangwin
|
|