4.2 Trigonometriska funktioner
Sommarmatte 1
| Versionen från 24 april 2007 kl. 13.56 (redigera) Lina (Diskussion | bidrag) (→Några standardvinklar) ← Gå till föregående ändring |
Nuvarande version (28 maj 2007 kl. 08.51) (redigera) (ogör) KTH.SE:u1qh5fat (Diskussion | bidrag) (→Några standardvinklar) |
||
| (45 mellanliggande versioner visas inte.) | |||
| Rad 1: | Rad 1: | ||
| + | __NOTOC__ | ||
| <table><tr><td width="600"> | <table><tr><td width="600"> | ||
| - | |||
| - | =4.2 Trigonometriska funktioner= | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| '''Innehåll:''' | '''Innehåll:''' | ||
| - | *De trigonometriska funktionerna cosinus, sinus och tangens | + | *De trigonometriska funktionerna cosinus, sinus och tangens. |
| </div> | </div> | ||
| <div class="inforuta"> | <div class="inforuta"> | ||
| - | '''Läromål:''' | + | '''Lärandemål:''' |
| Efter detta avsnitt ska du ha lärt dig att: | Efter detta avsnitt ska du ha lärt dig att: | ||
| - | *Förstå definitionen av cosinus, sinus och tangens i enhetscirkeln | + | *Känna till begreppen spetsig, trubbig och rät vinkel. |
| - | *Kunna utantill värdena på cosinus, sinus och tangens för standardvinklarna $ 0 $, $\pi/6$ , $\pi/4$ , $\pi/3$ och $\pi/2$ | + | *Förstå definitionen av cosinus, sinus och tangens i enhetscirkeln. |
| - | *Bestämma värdena på cosinus, sinus och tangens för argument som kan reduceras till standardvinklarna med periodicitet | + | *Utantill kunna värdena på cosinus, sinus och tangens för standardvinklarna $\,0\,$, $\,\pi/6\,$ , $\,\pi/4\,$ , $\,\pi/3\,$ och $\,\pi/2\,$. |
| - | *Skissera graferna till cosinus, sinus och tangens | + | *Bestämma värdena på cosinus, sinus och tangens för argument som kan reduceras till standardvinklarna i någon kvadrant av enhetscirkeln. |
| + | *Skissera graferna till cosinus, sinus och tangens. | ||
| + | *Lösa trigonometriska problem som involverar rätvinkliga trianglar. | ||
| </div> | </div> | ||
| Rad 31: | Rad 32: | ||
| =Teori= | =Teori= | ||
| ==Trigonometri i rätvinkliga trianglar== | ==Trigonometri i rätvinkliga trianglar== | ||
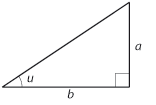
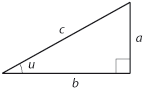
| - | I den rätvinkliga triangeln nedan kallas kvoten mellan den motstående kateten $a$ och den närliggande kateten $b$ för tangens av vinkeln $u$ och betecknas $\tan u$. | + | I den rätvinkliga triangeln nedan kallas kvoten mellan den motstående kateten $\,a\,$ och den närliggande kateten $\,b\,$ för tangens av vinkeln $\,u\,$ och betecknas $\,\tan u\,$. |
| - | Bild: figur 3.3.1 $\tan u = \displaystyle \frac{a}{b}$ | + | {| |
| - | + | |- | |
| - | Värdet på kvoten $\frac{a}{b}$ är inte beroende av storleken på triangeln utan bara på vinkeln $u$. För olika värden på vinkeln kan man få fram motsvarandet tangensvärde antingen i en trigonometrisk tabell eller genom att använda en miniräknare (knappen heter ofta tan). | + | | width=5% valign=top | |
| + | | width=50% valign=top | | ||
| + | [[Bild:t_3_3_1.gif]] | ||
| + | | width=45% valign=top | | ||
| + | <br> | ||
| + | $$\tan u = \displaystyle \frac{a}{b}$$ | ||
| + | |} | ||
| + | Värdet på kvoten $\,\frac{a}{b}\,$ är inte beroende av storleken på triangeln utan bara på vinkeln $\,u\,$. För olika värden på vinkeln kan man få fram motsvarande tangensvärde antingen i en trigonometrisk tabell eller genom att använda en miniräknare (knappen heter ofta tan). | ||
| <div class="exempel"> | <div class="exempel"> | ||
| Rad 43: | Rad 51: | ||
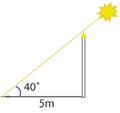
| Hur hög är flaggstången? | Hur hög är flaggstången? | ||
| - | Bild: figur 3.3.2 | + | [[Bild:t_3_3_2.gif|center]] |
| - | Flaggstången och dess skugga bildar tillsammans en rätvinklig triangel där den vertikala kateten är okänd (markerad med $x$ nedan). | + | Flaggstången och dess skugga bildar tillsammans en rätvinklig triangel där den vertikala kateten är okänd (markerad med $\,x\,$ nedan). |
| - | Bild: figur 3.3.3 | + | [[Bild:t_3_3_3.gif|center]] |
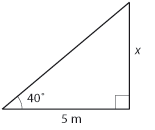
| Från definitionen av tangens har vi att | Från definitionen av tangens har vi att | ||
| $$\tan 40^\circ = \frac{x}{5 \mbox{ m }}$$ | $$\tan 40^\circ = \frac{x}{5 \mbox{ m }}$$ | ||
| - | och eftersom $\tan 40^\circ \approx 0{,}84$ så är | + | och eftersom $\,\tan 40^\circ \approx 0{,}84\,$ så är |
| - | $$x= 5\mbox{m} \cdot \tan 40^\circ \approx 5\mbox{m} \cdot 0{,}84 = 4{,}2 \mbox{m} \; \mbox{.}$$ | + | $$x= 5\,\mbox{m} \cdot \tan 40^\circ \approx 5\,\mbox{m} \cdot 0{,}84 = 4{,}2\,\mbox{m}\,\mbox{.}$$ |
| </div> | </div> | ||
| Rad 60: | Rad 68: | ||
| '''Exempel 2''' | '''Exempel 2''' | ||
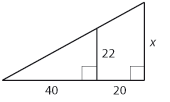
| - | Bestäm längden av sidan markerad med $x$ i figuren. | + | Bestäm längden av sidan markerad med $\,x\,$ i figuren. |
| - | Bild: figur 3.3.4 | + | [[Bild:t_3_3_4.gif|center]] |
| - | Om vi kallar vinkeln längst till vänster för $u$ så finns det två sätt att ställa upp ett uttryck för $\tan u$. | + | Om vi kallar vinkeln längst till vänster för $\,u\,$ så finns det två sätt att ställa upp ett uttryck för $\,\tan u\,$. |
| - | Bild: 3.3.5 (vänstermarignal) | + | {| |
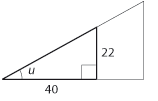
| - | $\tan u = \displaystyle \frac{22}{40}$ | + | |- |
| + | | width=5% valign=top | | ||
| + | | width=50% valign=top | | ||
| + | [[Bild:t_3_3_5.gif]] | ||
| + | | width=45% valign=top | | ||
| + | <br> | ||
| + | $$\tan u = \displaystyle \frac{22}{40}$$ | ||
| + | |} | ||
| - | Bild: 3.3.6 (vänstermarginal) | + | {| |
| + | |- | ||
| + | | width=5% valign=top | | ||
| + | | width=50% valign=top | | ||
| + | [[Bild:t_3_3_6.gif]] | ||
| + | | width=45% valign=top | | ||
| + | <br> | ||
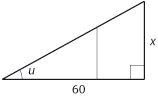
| + | $$\tan u = \displaystyle \frac{x}{60}$$ | ||
| + | |} | ||
| - | $\tan u = \displaystyle \frac{x}{60}$ | + | Sätter vi de två uttrycken för $\,\tan u\,$ lika fås |
| - | + | ||
| - | Sätter vi de två uttrycken för $\tan u$ lika fås | + | |
| $$\frac{22}{40} = \frac{x}{60}$$ | $$\frac{22}{40} = \frac{x}{60}$$ | ||
| - | vilket ger att $x=60 \cdot \displaystyle \frac{22}{40} = 33$. | + | vilket ger att $\,x=60 \cdot \displaystyle \frac{22}{40} = 33\,$. |
| </div> | </div> | ||
| - | Det finns två andra kvoter i rätvinkliga trianglar som har speciella namn och det är $\cos u = b/c$ ("cosinus av $u$") och $\sin u = a/c$ ("sinus av $u$"). | + | Det finns två andra kvoter i rätvinkliga trianglar som har speciella namn och det är $\,\cos u = b/c\,$ ("cosinus av $\,u\,$") och $\,\sin u = a/c\,$ ("sinus av $\,u\,$"). |
| - | Bild: figur 3.3.7 (vänstermarginal) | + | {| |
| + | |- | ||
| + | | width=5% valign=top | | ||
| + | | width=50% valign=top | | ||
| + | [[Bild:t_3_3_7.gif]] | ||
| + | | width=45% valign=top | | ||
| + | $$\eqalign{\cos u &= \displaystyle \frac{b}{c}\cr \sin u &= \displaystyle \frac{a}{c}}$$ | ||
| + | |} | ||
| - | $\cos u = \displaystyle \frac{b}{c}$ | + | Precis som för tangens är kvoterna som definierar cosinus och sinus inte beroende av triangelns storlek utan bara på vinkeln $\,u\,$. |
| - | + | ||
| - | $\sin u = \displaystyle \frac{a}{c}$ | + | |
| - | + | ||
| - | Precis som för tangens är kvoterna som definerar cosinus och sinus inte beroende av triangelns storlek utan bara på vinkeln $u$. | + | |
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 3''' | '''Exempel 3''' | ||
| - | Bild: figur 3.3.8 (vänstermarginal) | ||
| <ol type="a"> | <ol type="a"> | ||
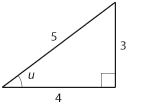
| - | <li>I triangel till vänster är | + | <li>[[Bild:t_3_3_8.gif|left]]I triangeln till vänster är |
| - | $$\cos u = \frac{4}{5}$$ | + | $$\eqalign{\cos u &= \textstyle\frac{4}{5}\cr \sin u &= \frac{3}{5}\cr}$$ |
| - | $$\sin u = \frac{3}{5}$$ | + | </ol><br><br> |
| - | </ol> | + | |
| - | Bild: figur 3.3.9 (vänstermarginal) | + | |
| <ol type="a" start=2> | <ol type="a" start=2> | ||
| - | <li>Definitionen av sinus ger att | + | <li>[[Bild:t_3_3_9.gif|left]]Definitionen av sinus ger att |
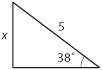
| $$\sin 38^\circ = \frac{x}{5}$$ | $$\sin 38^\circ = \frac{x}{5}$$ | ||
| - | och vet vi att $\sin 38^\circ \approx 0{,}616$ så får vi att | + | och vet vi att $\,\sin 38^\circ \approx 0{,}616\,$ så får vi att |
| - | $$x=5 \cdot \sin 38^\circ \approx 5 \cdot 0{,}616 \approx 3{,}1 \; \mbox{.}$$ | + | $$x=5 \cdot \sin 38^\circ \approx 5 \cdot 0{,}616 \approx 3{,}1\,\mbox{.}$$ |
| </ol> | </ol> | ||
| - | Bild: figur 3.3.10 (vänstermarginal) | ||
| <ol type="a" start=3> | <ol type="a" start=3> | ||
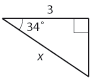
| - | <li>Cosinus är kvoten mellan den närliggande kateten och hypotenusan | + | <li>[[Bild:t_3_3_10.gif|left]]Cosinus är kvoten mellan den närliggande kateten och hypotenusan |
| - | $$\cos 34^\circ = \frac{3}{x}$$ | + | $$\cos 34^\circ = \frac{3}{x}\,\mbox{.}$$ |
| Alltså är | Alltså är | ||
| - | $$x=\frac{3}{\cos 34^\circ} \; \mbox{.}$$ | + | $$x=\frac{3}{\cos 34^\circ}\,\mbox{.}$$ |
| </ol> | </ol> | ||
| Rad 119: | Rad 139: | ||
| '''Exempel 4''' | '''Exempel 4''' | ||
| - | Bestäm $\sin u$ i triangeln Bild: figur 3.3.11 | + | Bestäm $\,\sin u\,$ i triangeln [[Bild:t_3_3_11.gif|center]] |
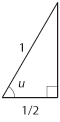
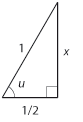
| Med hjälp av Pythagoras sats kan kateten till höger bestämmas | Med hjälp av Pythagoras sats kan kateten till höger bestämmas | ||
| - | Bild: figur 3.3.12 (vänster) | + | {| |
| + | |- | ||
| + | | width=5% valign=top | | ||
| + | | width=50% valign=top | | ||
| + | [[Bild:t_3_3_12.gif|left]] | ||
| + | | width=45% valign=top | | ||
| + | <br><br> | ||
| + | $$1^2= \bigl( \textstyle \frac{1}{2} \bigr)^2 + x^2\quad\Leftrightarrow\quad x= \displaystyle \frac{\sqrt{3}}{2}$$ | ||
| + | |} | ||
| - | $1^2= \left( \displaystyle \frac{1}{2} \right)^2 + x^2 \Leftrightarrow x= \displaystyle \frac{\sqrt{3}}{2}$ | + | och därför är $\,\sin u = \displaystyle \frac{\sqrt{3}/2}{1} = \displaystyle \frac{\sqrt{3}}{2}\,$. |
| - | + | ||
| - | och därför är $\sin u = \displaystyle \frac{\sqrt{3}/2}{1} = \displaystyle \frac{\sqrt{3}}{2}$. | + | |
| </div> | </div> | ||
| ==Några standardvinklar== | ==Några standardvinklar== | ||
| - | För vissa vinklar $30^\circ$, $45^\circ$ och $60^\circ$ går det relativt enkelt att räkna ut exakta värden på de trigonometriska funktionerna. | + | För vissa vinklar 30°, 45° och 60° går det relativt enkelt att räkna ut exakta värden på de trigonometriska funktionerna. |
| <div class="exempel"> | <div class="exempel"> | ||
| '''Exempel 5''' | '''Exempel 5''' | ||
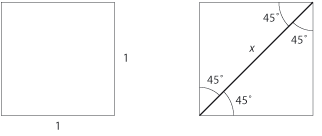
| - | Vi utgår från en kvadrat med sidlängd $1$. En diagonal i kvadraten delar de räta vinklarna i motsatt hörn i två lika delar $45^\circ$. | + | Vi utgår från en kvadrat med sidlängd 1. En diagonal i kvadraten delar de räta vinklarna i motsatta hörn i två lika delar 45°. |
| - | Bild: figur 3.3.13 | + | [[Bild:t_3_3_13.gif|center]] |
| - | Med Pythagoras sats kan vi bestämma diagonalens längd $x$, | + | Med Pythagoras sats kan vi bestämma diagonalens längd $\,x\,$, |
| - | $$x^2 = 1^2 + 1^2 \quad \Leftrightarrow \quad x = \sqrt{1^2 + 1^2} = \sqrt{2}\; \mbox{.}$$ | + | $$x^2 = 1^2 + 1^2 \quad \Leftrightarrow \quad x = \sqrt{1^2 + 1^2} = \sqrt{2}\,\mbox{.}$$ |
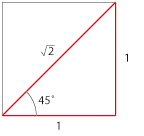
| I triangeln som har diagonalen som hypotenusa får vi fram värdet på de trigonometriska funktionerna för vinkeln $45^\circ$. | I triangeln som har diagonalen som hypotenusa får vi fram värdet på de trigonometriska funktionerna för vinkeln $45^\circ$. | ||
| - | Bild: 3.3.14 (vänstermarginal) | + | [[Bild:t_3_3_14.gif|left]]$$\eqalign{\cos 45^\circ &= \displaystyle \frac{1}{\sqrt{2}}\cr \sin 45^\circ &= \displaystyle \frac{1}{\sqrt{2}}\cr \tan 45^\circ &= \displaystyle \frac{1}{1}= 1\cr}$$ |
| - | + | ||
| - | $\cos 45^\circ = \displaystyle \frac{1}{\sqrt{2}}$ | + | |
| - | + | ||
| - | $\sin 45^\circ = \displaystyle \frac{1}{\sqrt{2}}$ | + | |
| - | + | ||
| - | $\tan 45^\circ = \displaystyle \frac{1}{1}= 1$ | + | |
| </div> | </div> | ||
| Rad 159: | Rad 179: | ||
| '''Exempel 6''' | '''Exempel 6''' | ||
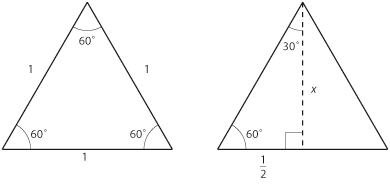
| - | Betrakta en liksidig triangel där alla sidor har längden $1$. Vinklarna i triangeln är alla $60^\circ$. Triangeln kan delas upp i två halvor av linjen som delar toppvinkeln mitt itu. | + | Betrakta en liksidig triangel där alla sidor har längd 1. Vinklarna i triangeln är alla 60°. Triangeln kan delas upp i två halvor av linjen som delar toppvinkeln mitt itu. |
| - | + | ||
| - | Bild: figurer 3.3.15 och 3.3.16 | + | |
| - | Pythagoras sats ger att den vertikala sidan av en triangelhalva är $x=\sqrt{3}/2$ (se figur). Från en triangelhalva får vi att | + | [[Bild:t_3_3_15.gif|center]] |
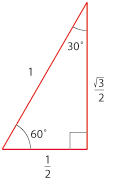
| - | Bild: figur 3.3.17 (vänstermarginal) | + | Pythagoras sats ger att den vertikala sidan av en triangelhalva är $\,x=\sqrt{3}/2\,$. Från en triangelhalva får vi att |
| - | $\cos 30^\circ = \displaystyle{\frac{\sqrt{3}/2}{1}}=\displaystyle{\frac{\sqrt{3}}{2}}\, ; \quad \cos 60^\circ = \displaystyle{\frac{1/2}{1}} =\displaystyle{\frac{1}{2}}$ | + | [[Bild:t_3_3_17.gif|left]] |
| - | $\sin 30^\circ = \displaystyle{\frac{1/2}{1}}=\displaystyle{\frac{1}{2}}\, ; \quad \sin 60^\circ = \displaystyle{\frac{\sqrt{3}/2}{1}} =\displaystyle{\frac{\sqrt{3}}{2}}$ | + | $$\eqalign{\displaystyle\cos 30^\circ &= \frac{\sqrt{3}/2}{1}=\frac{\sqrt{3}}{2}\,;\cr \sin 30^\circ &= \frac{1/2}{1}=\frac{1}{2}\,;\cr \tan 30^\circ &= \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}}\,;\cr}\qquad\quad \eqalign{\cos 60^\circ &= \frac{1/2}{1} = \frac{1}{2}\cr \sin 60^\circ &= \frac{\sqrt{3}/2}{1} =\frac{\sqrt{3}}{2}\cr \tan 60^\circ &= \frac{\sqrt{3}/2}{1/2}=\sqrt{3}}$$ |
| - | $\tan 30^\circ = \displaystyle{\frac{1/2}{\sqrt{3}/2}} =\displaystyle{\frac{1}{\sqrt{3}}}\, ; \quad \tan 60^\circ = \displaystyle{\frac{\sqrt{3}/2}{1/2}}=\sqrt{3}$ | ||
| </div> | </div> | ||
| ==Trigonometriska funktioner för allmänna vinklar== | ==Trigonometriska funktioner för allmänna vinklar== | ||
| - | ===Definitioner=== | + | För vinklar som är mindre än 0° eller större än 90° definieras de trigonometriska funktionerna med hjälp av enhetscirkeln (cirkeln som har medelpunkt i origo och radie 1). |
| + | <div class="regel"> | ||
| + | [[Bild:t_3_3_18.gif|right]] | ||
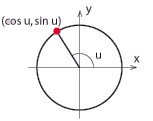
| + | De trigonometriska funktionerna $\,\cos u\,$ och $\,\sin u\,$ är ''x''- respektive ''y''-koordinaterna för skärningspunkten mellan enhetscirkeln och det radiella linjesegmentet som bildar vinkeln $\,u\,$ med den positiva ''x''-axeln. | ||
| - | De trigonometriska funktionerna sinus, cosinus och tangens definierades ursprungligen som förhållanden mellan de olika sidorna i en rätvinklig triangel. Denna definition har en nackdel: I en rätvinklig triangel finns inga negativa vinklar och inga vinklar större än $90^\circ$. | ||
| - | <img src="object49972/bilder/3_3/3_3_01.gif" align="right">Därför använder man ofta en alternativ definition som utgår från enhetscirkeln. En enhetscirkel är en cirkel med medelpunkten i origo och med radien 1. Enhetscirkeln har ekvationen $x^2 + y^2 = 1$ dvs alla punkter (x, y) på cirkeln uppfyller denna ekvation. Om en linje dras från origo till en godtycklig punkt på cirkeln så bildas en vinkel v mellan linjen och den positiva delen av x-axeln. De trigonometriska funktionerna sinus och cosinus definieras då som koordinaterna för punkten (x, y) som funktion av vinkeln ''v'' så att | ||
| - | $\cos v = x$ | ||
| + | </div> | ||
| - | och | + | Tangensfunktionen definieras som |
| + | $$\tan u = \displaystyle\frac{\sin u}{\cos u}$$ | ||
| - | $\sin v = y$. | + | och tangensvärdet kan tolkas som riktningskoefficienten för det radiella linjesegmentet. |
| - | Liksom tidigare gäller att $\tan v = \displaystyle\frac{\sin v}{\cos v}$. Tangens kan då tolkas som riktningskoefficienten för linjen som går från origo till punkten (x, y), och avläsas som ''y''-koordinaten för skärningspunkten mellan linjen och den lodräta linjen ''x'' = 1. Funktionen $\tan v$ är inte definierad då $\cos v = 0$. | ||
| + | <div class="exempel"> | ||
| + | '''Exempel 7''' | ||
| + | Från figurerna nedan avläser vi värdena på cosinus och sinus. | ||
| - | Definitionerna för sinus och cosinus i rätvinkliga trianglar (spetsiga vinklar) stämmer väl överens med denna definition och utgör då de specialfall då punkten befinner sig i första kvadranten. | ||
| + | <ol type="a"> | ||
| + | <li> | ||
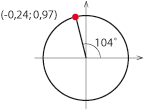
| + | [[Bild:3_3_19.gif|left]] | ||
| + | $\cos 104^\circ \approx -0{,}24$ <br><br> | ||
| + | $\sin 104^\circ \approx 0{,}97$ <br><br> | ||
| + | $\tan 104^\circ \approx \displaystyle \frac{0{,}97}{-0{,}24} \approx -4{,}0$ <br><br> | ||
| + | </ol> | ||
| + | <ol type="a" start=2> | ||
| + | <li> | ||
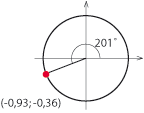
| + | [[Bild:3_3_20.gif|left]] | ||
| + | $\cos 201^\circ \approx -0{,}93$ <br><br> | ||
| + | $\sin 201^\circ \approx -0{,}36$ <br><br> | ||
| + | $\tan 201^\circ \approx \displaystyle \frac{-0{,}36}{-0{,}93} \approx 0{,}4$ | ||
| + | </ol> | ||
| + | </div> | ||
| - | För de trigonometriska funktionerna brukar vinkeln ''v'' anges i radianer. Då blir det lätt att derivera och integrera funktionerna. När vi betraktar sinus som en funktion brukar vi också byta namn på variabeln. Istället för att kalla vinkeln för ''v'' så kallar vi den för ''x'', eftersom den är indata till funktionen. Själva funktionsvärdet, $\sin x$, kan vi på samma sätt kalla för ''y''. Då kan vi rita upp funktionens graf i ett ''x, y''-koordinatsystem. Förväxla inte dessa ''x'' och ''y'' med dem i enhetscirkeln! | + | <div class="exempel"> |
| + | '''Exempel 8''' | ||
| + | Vilket tecken har | ||
| + | <ol type="a"> | ||
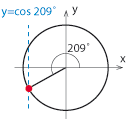
| + | <li>[[Bild:t_3_3_21.gif|right]]$\cos 209^\circ$ <br><br> | ||
| - | Det är viktigt att förstå hur man använder enhetscirkeln för att definiera de trigonometriska funktionerna. Enhetscirkeln är också mycket användbar för att komma ihåg många trigonometriska samband (avsnitt 3.4) och för att lösa trigonometriska ekvationer (avsnitt 3.5). | + | Eftersom vinkeln $\,209^\circ\,$ kan skrivas som $\,209^\circ = 180^\circ + 29^\circ\,$ så svarar vinkeln mot en punkt på enhetscirkeln som ligger i den tredje kvadranten. Den punkten har en negativ ''x''-koordinat, vilket betyder att $\,\cos 209^\circ\,$ är negativ. <br> |
| + | <br><br> | ||
| + | <li>[[Bild:t_3_3_22.gif|right]]$\sin 133^\circ$ <br><br> | ||
| + | Vinkeln $\,133^\circ\,$ är lika med $\,90^\circ + 43^\circ\,$ och ger en punkt på enhetscirkeln som ligger i den andra kvadranten. I den kvadranten har punkter positiv ''y''-koordinat och därför är $\,\sin 133^\circ\,$ positiv. <br> | ||
| + | <br><br> | ||
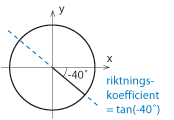
| + | <li>[[Bild:t_3_3_23.gif|right]]$\tan (-40^\circ)$ <br><br> | ||
| + | Ritas vinkeln $\,-40^\circ\,$ in i enhetscirkeln fås en vinkellinje som har en negativ riktningskoefficient, dvs. $\,\tan (-40^\circ)\,$ är negativ. <br> | ||
| + | <br><br> | ||
| + | </ol> | ||
| - | ==Det trigonometriska funktionernas grafer== | + | </div> |
| - | ===Grafer=== | + | <div class="exempel"> |
| + | '''Exempel 9''' | ||
| - | Sinus och cosinus kan med hjälp av enhetscirkeln definieras för alla värden på vinkeln ''v''. Experimentera gärna med cosinus och sinus i enhetscirkeln. <p align="left"><img src="ppStdFiles2261/774137.gif" hspace='0' vspace='0' /><br clear='all' /> | + | Bestäm $\ \sin \displaystyle \frac{2\pi}{3}\,$. |
| - | [http://www.math.kth.se/online/images/sinus_och_cosinus_i_enhetscirkeln.swf Interaktivt experiment: Sinus och cosinus i enhetscirkeln] | + | <br> |
| + | <br> | ||
| + | Omskrivningen | ||
| + | $$\frac{2\pi}{3} = \frac{4\pi}{6} = \frac{3\pi+ \pi}{6} = \frac{\pi}{2} + \frac{\pi}{6}$$ | ||
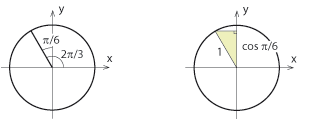
| - | Om vinkeln räknas moturs (positiv riktning) så är vinkeln positiv. Om vinkeln räknas medurs (negativ riktning) så är vinkeln negativ. Om vinkeln är större än $2\pi$ eller mindre än $–2 \pi$ , kan man "snurra" mer än ett varv i enhetscirkeln. Detta visar att de trigonometriska funktionerna är periodiska: Funktionsvärdena återkommer eftersom man för varje varv kommer tillbaka till samma punkter och därmed samma koordinater. Exempelvis innebär periodiciteten att | + | visar att vinkeln $\,2\pi/3\,$ hamnar i enhetscirkelns andra kvadrant och bildar vinkeln $\,\pi/6\,$ med den positiva ''y''-axeln. Om vi ritar in en hjälptriangel som i figuren nedan till höger så ser vi att $\,2\pi/3\,$-punkten på enhetscirkeln har en ''y''-koordinat som är lika med den närliggande kateten $\,\cos \frac{\pi}{6} = \sqrt{3}/2\,$. Alltså är |
| + | $$\sin\frac{2\pi}{3} = \frac{\sqrt{3}}{2}\,\mbox{.}$$ | ||
| + | [[Bild:t_3_3_24.gif|center]] | ||
| - | $\sin x = \sin(x + 2\pi) = \sin(x + 2\pi n)$ | + | </div> |
| + | ==De trigonometriska funktionernas grafer== | ||
| + | I förra avsnittet använde vi enhetscirkeln för att definiera cosinus och sinus för godtyckliga vinklar och vi kommer använda enhetscirkeln ofta framöver för att t.ex. härleda trigonometriska samband och lösa trigonometriska ekvationer. Det finns dock vissa egenskaper hos de trigonometriska funktionerna som bättre illustreras genom att rita upp deras funktionsgrafer. | ||
| - | där ''n'' är ett godtyckligt heltal. <p align="center"><img src="ppStdFiles2261/766673.gif" hspace='0' vspace='0' /><br clear='all' /> | + | [[Bild:3_3_03a.gif||center]] |
| + | [[Bild:3_3_03b.gif||center]] | ||
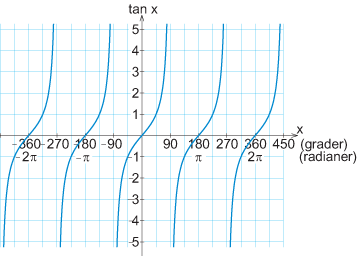
| - | Eftersom $\tan x = \displaystyle\frac{\sin x}{\cos x}$ så följer egenskaperna för denna funktion ur de egenskaper som vi gått igenom för $ \sin x $ och $\cos x$. Funktionen är därför också periodisk, men det visar sig att den blir periodisk med perioden $\pi$. Detta beror på att $\sin x = - \sin(x + \pi)$ och $\cos x = - \cos(x + \pi)$ och att minustecknen försvinner när vi dividerar. Alltså är $\tan x = \tan(x + \pi n)$ där ''n'' är ett godtyckligt heltal: <p align="center"><img src="ppStdFiles2261/766671.gif" hspace='0' vspace='0' /><br clear='all' /> | + | [[Bild:766671.gif||center]] |
| + | I graferna kan vi observera flera saker kanske tydligare än i enhetscirkeln. Några exempel är | ||
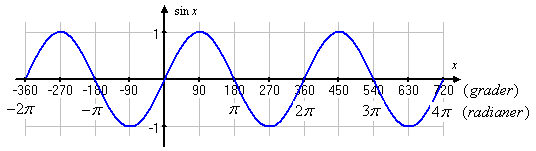
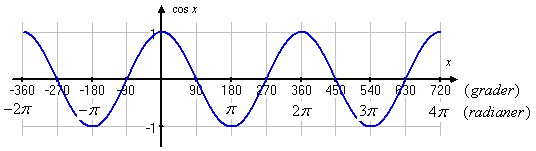
| - | Det är viktigt att kunna skissa graferna för de trigonometriska funktionerna. Trigonometriska ekvationer har ofta flera lösningar, och med en enkel skiss kan man få en uppfattning om hur många lösningar en ekvation har, och var man kan hitta lösningarna. | + | * Kurvorna för cosinus och sinus upprepar sig efter en vinkeländring på $\,2\pi\,$, dvs. det gäller att $\,\cos (x+2\pi) = \cos x\,$ och $\,\sin (x+2\pi) = \sin x\,$. I enhetscirkeln motsvarar $\,2\pi\,$ ett varv och efter ett helt varv återkommer vinklar till samma läge på enhetscirkeln och har därför samma koordinater. |
| + | *Kurvan för tangens upprepar sig redan efter en vinkeländring på $\,\pi\,$, dvs. $\,\tan (x+\pi) = \tan x\,$. Två vinklar som skiljer sig åt med $\,\pi\,$ ligger på samma linje genom origo i enhetscirkeln och deras vinkellinjer har därför samma riktningskoefficient. | ||
| + | |||
| + | *Förutom en fasförskjutning på $\pi/2$ är kurvorna för cosinus och sinus identiska, dvs. $\,\cos x = \sin (x+ \pi/2)\,$; mer om detta i nästa kapitel. | ||
| + | |||
| + | |||
| + | Graferna kan också vara viktiga när man undersöker trigonometriska ekvationer. Med en enkel skiss kan man ofta få en uppfattning om hur många lösningar en ekvation har, och var lösningarna finns. | ||
| + | |||
| + | <div class="exempel"> | ||
| + | '''Exempel 10''' | ||
| + | |||
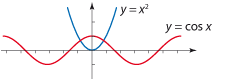
| + | Hur många lösningar har ekvationen $\,\cos x = x^2\,$? (där $x$ mäts i radianer) | ||
| + | <br> | ||
| + | <br> | ||
| + | Genom att rita upp graferna $\,y=\cos x\,$ och $\,y=x^2\,$ ser vi att kurvorna skär varandra i två punkter. Det finns alltså två ''x''-värden för vilka motsvarande ''y''-värden är lika. Med andra ord har ekvationen två lösningar. | ||
| + | |||
| + | [[Bild:t_3_3_25.gif||center]] | ||
| + | |||
| + | </div> | ||
| + | |||
| + | [[4.2 Övningar|Övningar]] | ||
| + | |||
| <div class="inforuta"> | <div class="inforuta"> | ||
| '''Råd för inläsning''' | '''Råd för inläsning''' | ||
| + | |||
| + | '''Grund- och slutprov''' | ||
| + | |||
| + | Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge. | ||
| + | |||
| '''Tänk på att:''' | '''Tänk på att:''' | ||
| Rad 260: | Rad 343: | ||
| </div> | </div> | ||
| - | |||
| - | |||
| - | '''© Copyright 2006, KTH Matematik''' | ||
| - | |||
| - | |||
Nuvarande version
|
Innehåll:
Lärandemål: Efter detta avsnitt ska du ha lärt dig att:
|
||||||||||||||||
[redigera] Teori[redigera] Trigonometri i rätvinkliga trianglarI den rätvinkliga triangeln nedan kallas kvoten mellan den motstående kateten $\,a\,$ och den närliggande kateten $\,b\,$ för tangens av vinkeln $\,u\,$ och betecknas $\,\tan u\,$.
Värdet på kvoten $\,\frac{a}{b}\,$ är inte beroende av storleken på triangeln utan bara på vinkeln $\,u\,$. För olika värden på vinkeln kan man få fram motsvarande tangensvärde antingen i en trigonometrisk tabell eller genom att använda en miniräknare (knappen heter ofta tan). Exempel 1 Hur hög är flaggstången? Flaggstången och dess skugga bildar tillsammans en rätvinklig triangel där den vertikala kateten är okänd (markerad med $\,x\,$ nedan). Från definitionen av tangens har vi att $$\tan 40^\circ = \frac{x}{5 \mbox{ m }}$$ och eftersom $\,\tan 40^\circ \approx 0{,}84\,$ så är $$x= 5\,\mbox{m} \cdot \tan 40^\circ \approx 5\,\mbox{m} \cdot 0{,}84 = 4{,}2\,\mbox{m}\,\mbox{.}$$ Exempel 2 Bestäm längden av sidan markerad med $\,x\,$ i figuren. Om vi kallar vinkeln längst till vänster för $\,u\,$ så finns det två sätt att ställa upp ett uttryck för $\,\tan u\,$.
Sätter vi de två uttrycken för $\,\tan u\,$ lika fås $$\frac{22}{40} = \frac{x}{60}$$ vilket ger att $\,x=60 \cdot \displaystyle \frac{22}{40} = 33\,$. Det finns två andra kvoter i rätvinkliga trianglar som har speciella namn och det är $\,\cos u = b/c\,$ ("cosinus av $\,u\,$") och $\,\sin u = a/c\,$ ("sinus av $\,u\,$").
Precis som för tangens är kvoterna som definierar cosinus och sinus inte beroende av triangelns storlek utan bara på vinkeln $\,u\,$. Exempel 3
Exempel 4 Bestäm $\,\sin u\,$ i triangelnMed hjälp av Pythagoras sats kan kateten till höger bestämmas
och därför är $\,\sin u = \displaystyle \frac{\sqrt{3}/2}{1} = \displaystyle \frac{\sqrt{3}}{2}\,$. [redigera] Några standardvinklarFör vissa vinklar 30°, 45° och 60° går det relativt enkelt att räkna ut exakta värden på de trigonometriska funktionerna. Exempel 5 Vi utgår från en kvadrat med sidlängd 1. En diagonal i kvadraten delar de räta vinklarna i motsatta hörn i två lika delar 45°. Med Pythagoras sats kan vi bestämma diagonalens längd $\,x\,$, $$x^2 = 1^2 + 1^2 \quad \Leftrightarrow \quad x = \sqrt{1^2 + 1^2} = \sqrt{2}\,\mbox{.}$$ I triangeln som har diagonalen som hypotenusa får vi fram värdet på de trigonometriska funktionerna för vinkeln $45^\circ$. $$\eqalign{\cos 45^\circ &= \displaystyle \frac{1}{\sqrt{2}}\cr \sin 45^\circ &= \displaystyle \frac{1}{\sqrt{2}}\cr \tan 45^\circ &= \displaystyle \frac{1}{1}= 1\cr}$$Exempel 6 Betrakta en liksidig triangel där alla sidor har längd 1. Vinklarna i triangeln är alla 60°. Triangeln kan delas upp i två halvor av linjen som delar toppvinkeln mitt itu. Pythagoras sats ger att den vertikala sidan av en triangelhalva är $\,x=\sqrt{3}/2\,$. Från en triangelhalva får vi att $$\eqalign{\displaystyle\cos 30^\circ &= \frac{\sqrt{3}/2}{1}=\frac{\sqrt{3}}{2}\,;\cr \sin 30^\circ &= \frac{1/2}{1}=\frac{1}{2}\,;\cr \tan 30^\circ &= \frac{1/2}{\sqrt{3}/2} = \frac{1}{\sqrt{3}}\,;\cr}\qquad\quad \eqalign{\cos 60^\circ &= \frac{1/2}{1} = \frac{1}{2}\cr \sin 60^\circ &= \frac{\sqrt{3}/2}{1} =\frac{\sqrt{3}}{2}\cr \tan 60^\circ &= \frac{\sqrt{3}/2}{1/2}=\sqrt{3}}$$
[redigera] Trigonometriska funktioner för allmänna vinklarFör vinklar som är mindre än 0° eller större än 90° definieras de trigonometriska funktionerna med hjälp av enhetscirkeln (cirkeln som har medelpunkt i origo och radie 1). De trigonometriska funktionerna $\,\cos u\,$ och $\,\sin u\,$ är x- respektive y-koordinaterna för skärningspunkten mellan enhetscirkeln och det radiella linjesegmentet som bildar vinkeln $\,u\,$ med den positiva x-axeln.
Tangensfunktionen definieras som $$\tan u = \displaystyle\frac{\sin u}{\cos u}$$ och tangensvärdet kan tolkas som riktningskoefficienten för det radiella linjesegmentet.
Exempel 7 Från figurerna nedan avläser vi värdena på cosinus och sinus.
Exempel 8 Vilket tecken har
Exempel 9 Bestäm $\ \sin \displaystyle \frac{2\pi}{3}\,$.
visar att vinkeln $\,2\pi/3\,$ hamnar i enhetscirkelns andra kvadrant och bildar vinkeln $\,\pi/6\,$ med den positiva y-axeln. Om vi ritar in en hjälptriangel som i figuren nedan till höger så ser vi att $\,2\pi/3\,$-punkten på enhetscirkeln har en y-koordinat som är lika med den närliggande kateten $\,\cos \frac{\pi}{6} = \sqrt{3}/2\,$. Alltså är $$\sin\frac{2\pi}{3} = \frac{\sqrt{3}}{2}\,\mbox{.}$$ [redigera] De trigonometriska funktionernas graferI förra avsnittet använde vi enhetscirkeln för att definiera cosinus och sinus för godtyckliga vinklar och vi kommer använda enhetscirkeln ofta framöver för att t.ex. härleda trigonometriska samband och lösa trigonometriska ekvationer. Det finns dock vissa egenskaper hos de trigonometriska funktionerna som bättre illustreras genom att rita upp deras funktionsgrafer. I graferna kan vi observera flera saker kanske tydligare än i enhetscirkeln. Några exempel är
Exempel 10 Hur många lösningar har ekvationen $\,\cos x = x^2\,$? (där $x$ mäts i radianer)
Råd för inläsning Grund- och slutprov Efter att du har läst texten och arbetat med övningarna ska du göra grund- och slutprovet för att bli godkänd på detta avsnitt. Du hittar länken till proven i din student lounge.
Har du läst trigonometri, så ska du inte vara rädd för att använda den i geometriska problem. Det ger ofta en enklare lösning. Du kan behöva lägga ner mycket tid på att förstå hur man använder enhetscirkeln för att definiera de trigonometriska funktionerna. Ta för vana att räkna med exakta trigonometriska värden. Det ger en bra träning på bråkräkning och så småningom i räkning med algebraiska rationella uttryck.
för dig som vill fördjupa dig ytterligare eller behöver en längre förklaring vill vi tipsa om: Läs mer om Trigonometri i Per Edströms "Interaktiv Matematik" Läs mer om trigonometri på engelska Wikipedia Läs mer om enhetscirkeln på engelska Wikipedia
|
|