From Förberedande kurs i matematik 1

Let's write down the equation for a straight line as

\displaystyle y=kx+m\,,

where k and m are constants which we shall determine.

Since the points (2,3) and (3,0) should lie on the line, they must also satisfy the equation of the line,

\displaystyle 3=k\cdot 2+m\qquad\text{and}\qquad 0=k\cdot 3+m\,\textrm{.}

If we take the difference between the equations, m disappears and we can work out the slope k,

\displaystyle \begin{align} 3-0 &= k\cdot 2+m-(k\cdot 3+m)\,,\\[5pt] 3 &= -k\,\textrm{.} \end{align}

Substituting this into the equation \displaystyle 0=k\centerdot 3+m then gives us a value for m,

\displaystyle m=-3k=-3\cdot (-3)=9\,\textrm{.}

The equation of the line is thus \displaystyle y=-3x+9.

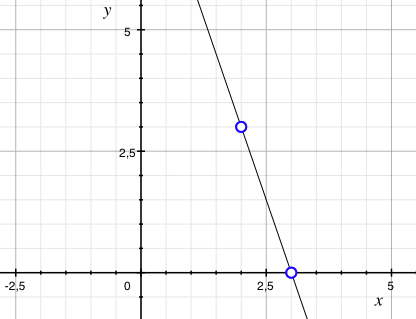
Note. To be completely certain that we have calculated correctly, we check that the points (2,3) and (3,0) satisfy the equation of the line:

• (x,y) = (2,3): \displaystyle \text{LHS} = 3\ and \displaystyle \ \text{RHS} = -3\cdot 2+9 = 3\,.
• (x,y) = (3,0): \displaystyle \text{LHS} = 0\ and \displaystyle \ \text{LHS} = -3\cdot 3+9 = 0\,.