From Förberedande kurs i matematik 1

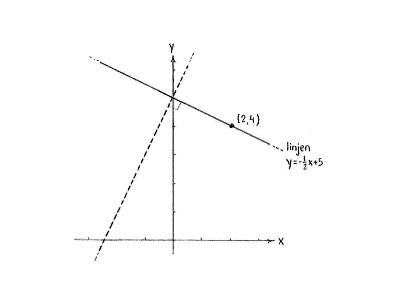
If two non-vertical lines are perpendicular to each other, their slopes \displaystyle k_{1} and \displaystyle k_{2} satisfy the relation \displaystyle k_{1}k_{2}=-1, and from this we have that the line we are looking for must have a slope that is given by

\displaystyle k_{2} = -\frac{1}{k_{1}} = -\frac{1}{2}

since the line \displaystyle y=2x+5 has a slope \displaystyle k_{1}=2 (the coefficient in front of x).

The line we are looking for can thus be written in the form

\displaystyle y=-\frac{1}{2}x+m

with m as an unknown constant.

Because the point (2,4) should lie on the line, (2,4) must satisfy the equation of the line,

\displaystyle 4=-\frac{1}{2}\cdot 2+m\,,

i.e. \displaystyle m=5. The equation of the line is \displaystyle y=-\frac{1}{2}x+5.