From Förberedande kurs i matematik 1

First, let's decide to determine all distance in dm (decimeters), so that we have all the distances as integers.

Call the length of the washing line from the trees to the hanger y and z, as in the figure below, and introduce two auxiliary triangles which have y and z as their hypotenuses. (As an approximation, we suppose that the taut washing line consists of two straight parts.)

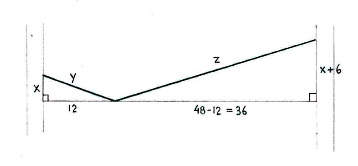
Because the line is 54 dm long, we have

\displaystyle y+z=54\,\textrm{.}

(1)

Then, the Pythagorean theorem gives the relations

\displaystyle y^2 = x^2 + 12^2\,,

(2)

\displaystyle z^2 = (x+6)^2 + 36^2\,\textrm{.}

(3)

The idea now is to solve the system of equations (1)-(3) by first eliminating z, so that we get two equations which only contain x and y. Then, eliminate y from one of these equations, so that we get an equation which determines x.

From (1), we have \displaystyle z = 54-y, and substituting this into (3) gives us the equation

\displaystyle (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.}

(3')

Equations (2) and (3') together give a smaller system for x and y,

\displaystyle \left\{ \begin{align} & y^2 = x^2 + 12^2\,,\\[5pt] & (54-y)^2 = (x+6)^2 + 36^2\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3')\end{align}

Expand the quadratic terms on both sides of (3'),

\displaystyle 54^2 - 2\cdot 54\cdot y + y^2 = x^2 + 2\cdot 6\cdot x + 6^2 + 36^2\,,

and simplify

\displaystyle 2916 - 108y + y^2 = x^2 + 12x + 1332\,\textrm{.}

Use (2) and replace \displaystyle y^2 with \displaystyle x^2+12 in this equation,

\displaystyle 2916 - 108y + x^2 + 144 = x^2 + 12x + 1332

which gets rid of the x²-term,

\displaystyle 2916 - 108y + 144 = 12x + 1332\,,

and further simplification gives the equation

\displaystyle 12x + 108y = 1728

(3")

If we pause for a moment and summarize the situation, we see that we have succeeded in simplifying the equation system (2) and (3') to a system (2) and (3"), where one of the equations is linear

\displaystyle \left\{ \begin{align} & y^2 = x^2 + 12^2\,,\\[5pt] & 12x+108y=1728\,\textrm{.} \end{align} \right.

\displaystyle \begin{align}(2)\\[5pt] (3")\end{align}

In this system, we can make y the subject in (3"),

\displaystyle y=\frac{1728-12x}{108}=16-\frac{x}{9}

and substitute into (2),

\displaystyle \Bigl(16-\frac{x}{9}\Bigr)^2 = x^2 + 144\,\textrm{.}

This is an equation which only contains x, and if we solve it, we will get our answer.

Expand the quadratic on the left-hand side,

\displaystyle 16^{2}-2\cdot 16\cdot \frac{x}{9} + \Bigl(\frac{x}{9} \Bigr)^2 = x^2 + 144

and collect together all terms on one side,

\displaystyle x^2 - \frac{x^{2}}{81} + \frac{32}{9}x + 144 - 16^{2} = 0\,,

which gives the equation

\displaystyle \frac{80}{81}x^2 + \frac{32}{9}x - 112 = 0\,\textrm{.}

Multiply both sides by \displaystyle 81/80 so that we get the equation in standard form,

\displaystyle x^{2} + \frac{18}{5}x - \frac{567}{5} = 0\,\textrm{.}

Completing the square on the left-hand side gives

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 - \Bigl(\frac{9}{5}\Bigr)^{2} - \frac{567}{5} = 0

and then

\displaystyle \Bigl(x+\frac{9}{5}\Bigr)^2 = \frac{81}{25} + \frac{567}{5} = \frac{2916}{25}\,,

i.e.

\displaystyle x = -\frac{9}{5}\pm \sqrt{\frac{2916}{25}} = -\frac{9}{5}\pm \frac{54}{5}\,\textrm{.}

This means that the equation has the solutions

\displaystyle x=-\frac{9}{5}-\frac{54}{5}=-\frac{63}{5}\qquad\text{and}\qquad x=-\frac{9}{5}+\frac{54}{5}=9\,\textrm{.}

The answer is thus \displaystyle x=9\ \textrm{dm} (the negative root must be discarded).

To be sure that we have calculated correctly, we also look at the values of y and z, and check that the original equations (1) to (3) are satisfied.

Equation (3") gives

\displaystyle y = 16-\frac{x}{9} = 16-1 = 15

and equation (1) gives

\displaystyle z=54-y=54-15=39\,\textrm{.}

Now, we check that \displaystyle x=9, \displaystyle y=15 and \displaystyle z=39 satisfy the equations (1), (2) and (3),

\displaystyle \begin{align} \textrm{LHS of (1)} &= 15+39 = 54\,,\\[5pt] \textrm{RHS of (1)} &= 54\,,\\[10pt] \textrm{LHS of (2)} &= 15^2 = 225\,,\\[5pt] \textrm{RHS of (2)} &= 9^2 + 12^2 = 81+144 = 225\,,\\[10pt] \textrm{LHS of (3)} &= 39^2 = 1521\,,\\[5pt] \textrm{RHS of (3)} &= (9+6)^2 + 36^2 = 15^2 + 36^2 = 225+1296 = 1521\,\textrm{.} \end{align}