From Förberedande kurs i matematik 1

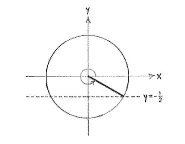
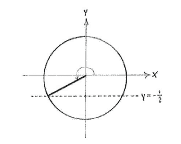
We can translate the equation \displaystyle \sin v=-1/2 to the problem of finding those angles in the unit circle which have a y-coordinate of \displaystyle -1/2. If we compare this with the problem that we had in exercise a, where we looked for angles which satisfied \displaystyle \sin v = +1/2, then the situation is the same, except that the angles now lie under, rather than above, the x-axis, due to reflectional symmetry.

Angle 2π - π/6 = 11π/6		Angle π + π/6 = 7π/6

The two angles which satisfy \displaystyle \sin v=-1/2 lie in the third and fourth quadrants and are \displaystyle v=2\pi - \pi/6 = 11\pi/6 and \displaystyle v = \pi + \pi/6 = 7\pi/6.