From Förberedande kurs i matematik 1

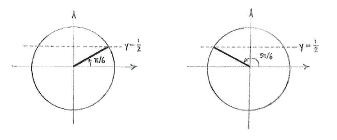
This is almost the same equation as in exercise d. First, we determine the solutions to the equation when \displaystyle 0\le 5x\le 2\pi, and using the unit circle shows that there are two of these,

\displaystyle 5x = \frac{\pi}{6}\qquad\text{and}\qquad 5x = \pi - \frac{\pi}{6} = \frac{5\pi}{6}\,\textrm{.}

We obtain the remaining solutions by adding multiples of \displaystyle 2\pi to the two solutions above,

\displaystyle 5x = \frac{\pi}{6} + 2n\pi\qquad\text{and}\qquad 5x = \frac{5\pi}{6} + 2n\pi\,,

where n is an arbitrary integer, or if we divide by 5,

\displaystyle x = \frac{\pi}{30} + \frac{2}{5}n\pi\qquad\text{and}\qquad x = \frac{\pi}{6} + \frac{2}{5}n\pi\,,

where n is an arbitrary integer.