Processing Math: Done
Solution 4.4:6c
From Förberedande kurs i matematik 1
If we use the trigonometric relation
In exercise 4.4:5a, we saw that an equality of the type
is satisfied if
 oru= oru= −v+2n −v+2n  |
where n is an arbitrary integer. The consequence of this is that the solutions to the equation satisfy
 or2x= or2x= −(−x)+2n −(−x)+2n  |
i.e.
 orx= orx= +2n +2n . . |
The solutions to the equation are thus
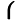 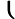 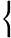 xx=32n xx=32n  = = +2n +2n  |
where n is an arbitrary integer.
