Processing Math: Done

From Förberedande kurs i matematik 1

Revision as of 14:46, 31 March 2008 (edit) Lina (Talk | contribs) (Ny sida: {{NAVCONTENT_START}} <center> Bild:2_2_5a-1(2).gif </center> {{NAVCONTENT_STOP}} {{NAVCONTENT_START}} <center> Bild:2_2_5a-2(2).gif </center> {{NAVCONTENT_STOP}}) ← Previous diff		Current revision (11:55, 24 September 2008) (edit) (undo) Tek (Talk | contribs) m
(6 intermediate revisions not shown.)
Line 1:		Line 1:
-	{{NAVCONTENT_START}}	+	Let's write down the equation for a straight line as
-	<center> [[Bild:2_2_5a-1(2).gif]] </center>	+
-	{{NAVCONTENT_STOP}}	+	{{Displayed math||<math>y=kx+m\,,</math>}}
-	{{NAVCONTENT_START}}	+
-	<center> [[Bild:2_2_5a-2(2).gif]] </center>	+	where ''k'' and ''m'' are constants which we shall determine.
-	{{NAVCONTENT_STOP}}	+
		+	Since the points (2,3) and (3,0) should lie on the line, they must also satisfy the equation of the line,
		+
		+	{{Displayed math||<math>3=k\cdot 2+m\qquad\text{and}\qquad 0=k\cdot 3+m\,\textrm{.}</math>}}
		+
		+	If we take the difference between the equations, ''m'' disappears and we can work out the slope ''k'',
		+
		+	{{Displayed math||<math>\begin{align}
		+	3-0 &= k\cdot 2+m-(k\cdot 3+m)\,,\\[5pt]
		+	3 &= -k\,\textrm{.}
		+	\end{align}</math>}}
		+
		+	Substituting this into the equation <math>0=k\centerdot 3+m</math> then gives us a value for ''m'',
		+
		+	{{Displayed math||<math>m=-3k=-3\cdot (-3)=9\,\textrm{.}</math>}}
		+
		+	The equation of the line is thus <math>y=-3x+9</math>.
		+
		+
		+	<center>[[Image:S1_2_2_5_a.jpg]]</center>
		+
		+
		+	Note. To be completely certain that we have calculated correctly, we check that the points (2,3) and (3,0) satisfy the equation of the line:
		+
		+	:*(''x'',''y'')&nbsp;=&nbsp;(2,3): <math>\text{LHS} = 3\ </math> and <math>\ \text{RHS} = -3\cdot 2+9 = 3\,</math>.
		+	:*(''x'',''y'')&nbsp;=&nbsp;(3,0): <math>\text{LHS} = 0\ </math> and <math>\ \text{LHS} = -3\cdot 3+9 = 0\,</math>.

---

Current revision

Let's write down the equation for a straight line as

y=kx+m

where k and m are constants which we shall determine.

Since the points (2,3) and (3,0) should lie on the line, they must also satisfy the equation of the line,

3=k2+mand0=k3+m.

If we take the difference between the equations, m disappears and we can work out the slope k,

3−03=k2+m−(k3+m)=−k.

Substituting this into the equation 0=k3+m then gives us a value for m,

m=−3k=−3(−3)=9.

The equation of the line is thus y=−3x+9.

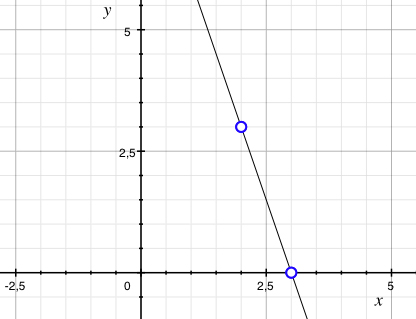
Note. To be completely certain that we have calculated correctly, we check that the points (2,3) and (3,0) satisfy the equation of the line:

• (x,y) = (2,3): LHS=3  and  RHS=−32+9=3.
• (x,y) = (3,0): LHS=0  and  LHS=−33+9=0.