Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Solution 2.2:5d

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (12:44, 24 September 2008) (edit) (undo)
m
 
(5 intermediate revisions not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
If two non-vertical lines are perpendicular to each other, their slopes <math>k_{1}</math> and <math>k_{2}</math> satisfy the relation <math>k_{1}k_{2}=-1</math>, and from this we have that the line we are looking for must have a slope that is given by
-
<center> [[Bild:2_2_5d-1(2).gif]] </center>
+
 
-
{{NAVCONTENT_STOP}}
+
{{Displayed math||<math>k_{2} = -\frac{1}{k_{1}} = -\frac{1}{2}</math>}}
-
{{NAVCONTENT_START}}
+
 
-
<center> [[Bild:2_2_5d-2(2).gif]] </center>
+
since the line <math>y=2x+5</math> has a slope <math>k_{1}=2</math>
-
{{NAVCONTENT_STOP}}
+
(the coefficient in front of ''x'').
 +
 
 +
The line we are looking for can thus be written in the form
 +
 
 +
{{Displayed math||<math>y=-\frac{1}{2}x+m</math>}}
 +
 
 +
with ''m'' as an unknown constant.
 +
 
 +
Because the point (2,4) should lie on the line, (2,4) must satisfy the equation of the line,
 +
 
 +
{{Displayed math||<math>4=-\frac{1}{2}\cdot 2+m\,,</math>}}
 +
 
 +
i.e. <math>m=5</math>. The equation of the line is <math>y=-\frac{1}{2}x+5</math>.
 +
 
 +
 
 +
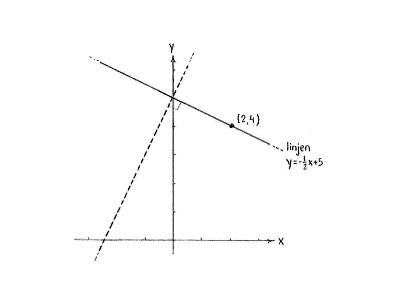
<center>[[Image:2_2_5d-2(2).gif]]</center>

Current revision

If two non-vertical lines are perpendicular to each other, their slopes k1 and k2 satisfy the relation k1k2=−1, and from this we have that the line we are looking for must have a slope that is given by

k2=−1k1=−21

since the line y=2x+5 has a slope k1=2 (the coefficient in front of x).

The line we are looking for can thus be written in the form

y=−21x+m

with m as an unknown constant.

Because the point (2,4) should lie on the line, (2,4) must satisfy the equation of the line,

4=−212+m

i.e. m=5. The equation of the line is y=−21x+5.


Image:2_2_5d-2(2).gif
Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_2.2:5d"