Solution 2.2:6d

From Förberedande kurs i matematik 1

(Difference between revisions)
Jump to: navigation, search
Current revision (13:14, 24 September 2008) (edit) (undo)
m
 
(4 intermediate revisions not shown.)
Line 1: Line 1:
-
{{NAVCONTENT_START}}
+
At the point where the lines cut each other, we have a point that lies on both lines and which must therefore satisfy the equations of both lines,
-
[[Bild:2_2_6_d.gif]]
+
 
-
<center> [[Bild:2_2_6d.gif]] </center>
+
{{Displayed math||<math>x+y+1=0\qquad\text{and}\qquad x=12\,\textrm{.}</math>}}
-
{{NAVCONTENT_STOP}}
+
 
 +
We obtain the solution to this system of equations by substituting <math>x=12</math>
 +
into the first equation
 +
 
 +
{{Displayed math||<math>12+y+1=0\quad\Leftrightarrow\quad y=-13\,\textrm{,}</math>}}
 +
 
 +
which gives us the point of intersection as (12,-13).
 +
 
 +
 
 +
<center>[[Image:2_2_6_d.gif|center]]</center>

Current revision

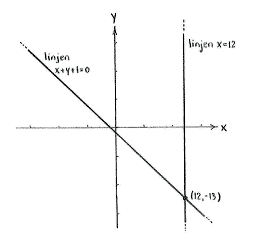
At the point where the lines cut each other, we have a point that lies on both lines and which must therefore satisfy the equations of both lines,

\displaystyle x+y+1=0\qquad\text{and}\qquad x=12\,\textrm{.}

We obtain the solution to this system of equations by substituting \displaystyle x=12 into the first equation

\displaystyle 12+y+1=0\quad\Leftrightarrow\quad y=-13\,\textrm{,}

which gives us the point of intersection as (12,-13).


Retrieved from "http://wiki.math.se/wikis/2008/bridgecourse1-ImperialCollege/index.php/Solution_2.2:6d"