Processing Math: Done
Solution 4.4:2e
From Förberedande kurs i matematik 1
(Difference between revisions)
m (Lösning 4.4:2e moved to Solution 4.4:2e: Robot: moved page) |
m |
||
| (One intermediate revision not shown.) | |||
| Line 1: | Line 1: | ||
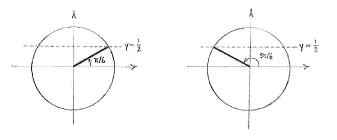
| - | + | This is almost the same equation as in exercise d. First, we determine the solutions to the equation when <math>0\le 5x\le 2\pi</math>, and using the unit circle shows that there are two of these, | |
| - | < | + | |
| - | {{ | + | {{Displayed math||<math>5x = \frac{\pi}{6}\qquad\text{and}\qquad 5x = \pi - \frac{\pi}{6} = \frac{5\pi}{6}\,\textrm{.}</math>}} |
[[Image:4_4_2_e.gif|center]] | [[Image:4_4_2_e.gif|center]] | ||
| + | |||
| + | We obtain the remaining solutions by adding multiples of <math>2\pi</math> to the two solutions above, | ||
| + | |||
| + | {{Displayed math||<math>5x = \frac{\pi}{6} + 2n\pi\qquad\text{and}\qquad 5x = \frac{5\pi}{6} + 2n\pi\,,</math>}} | ||
| + | |||
| + | where ''n'' is an arbitrary integer, or if we divide by 5, | ||
| + | |||
| + | {{Displayed math||<math>x = \frac{\pi}{30} + \frac{2}{5}n\pi\qquad\text{and}\qquad x = \frac{\pi}{6} + \frac{2}{5}n\pi\,,</math>}} | ||
| + | |||
| + | where ''n'' is an arbitrary integer. | ||
Current revision
This is almost the same equation as in exercise d. First, we determine the solutions to the equation when 
5x2
| 6and5x=−6=65. |
We obtain the remaining solutions by adding multiples of
6+2nand5x=65+2n |
where n is an arbitrary integer, or if we divide by 5,
| 30+52nandx=6+52n |
where n is an arbitrary integer.
