Processing Math: Done
Tips och lösning till övning 17.13
SamverkanLinalgLIU
Tips 1
Rita figur enl exempel 16.17
Tips 2
Av figuren ser du att speglingen av vektorn u = u:s projektion i planet - 2 gånger u:s projektion på normalvektorn.
Tips 3
 )=
)= −2
−2

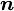

 2(
2(

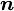 )
)
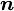
Lösning
Speglingen  =(x1
=(x1 x2
x2 x3)t
x3)t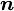 =(1
=(1 1
1 1)t
1)t
 )=
)= −2
−2

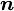

 2(
2(

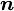 )
)
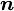 =
=

 x1x2x3
x1x2x3

 −32
−32

 x1+x2+x3x1+x2+x3x1+x2+x3
x1+x2+x3x1+x2+x3x1+x2+x3

 =31
=31

 x1−2x2−2x3x1−2x2−2x3x1−2x2−2x3
x1−2x2−2x3x1−2x2−2x3x1−2x2−2x3

 =31
=31

 1−2−2−21−2−2−21
1−2−2−21−2−2−21




 x1x2x3
x1x2x3



Matrisen är därmed 

 1−2−2−21−2−2−21
1−2−2−21−2−2−21


