Tips och lösning till övning 3.11b
SamverkanLinalgLIU
Tips 1
Tänk geometriskt! Rita gärna en liten figur.
Tips 2
De vektorer som ligger i båda planen ligger i skärningslinjen mellan de två planen..
Tips 3
Du får ett ekvationssystem att lösa som består av de två planens ekvationer. Glöm ej att jämföra det resultat du får med de geometriska tänk du startade med. Vidare kan du kontrollera att din vektor ligger i båda planen, dvs att koordinaterna uppfyller ekvationenerna för de två planen.
Lösning
Snittmängden  W
W
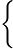 2x1−3x2+x317x1−28x2+8x3==00
2x1−3x2+x317x1−28x2+8x3==00
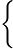 2x1−3x2+x35x2+x3==00
2x1−3x2+x35x2+x3==00
Vi sätter x
 W
W
 =t
=t

 41−5
41−5



 W=
W=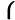


 :
:  =t
=t

 41−5
41−5


 t
t R
R