Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Tips och lösning till övning 3.18a

SamverkanLinalgLIU

Hoppa till: navigering, sök

Tips 1

Tänk efter vad som krävs för att de tre vektorerna skall bilda en bas.

Tips 2

Vektorn 3 skall alltså ej vara en linjärkombination av 1 och 2.Vi formulerar därför ett villkor som 3 ej skall uppfylla.

Tips 3

3=x1x2x3 är en linjärkombination av 1 och 2 om 11+23=31110+211−1=x1x2x3.

Lös nu detta ekvationssystem!

Lösning


Vektorn 3 ska alltså inte vara en linjärkombination i 1 och 2, dvs 3 ska inte ligga i planet U som spänns upp av 1 och 2.

En vektor 3=x1x2x3U om

11+23=31110+211−1=x1x2x3

dvs

11011−1x1x2x310010−1x1x2−x1x3

Alltså måste vi välja

3=x1x2x3U=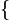x1−x2=0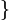

så att 1 , 2 och 3 blir linjärt oberoende och därmed en bas för rummet.

Den här artikeln är hämtad från http://wiki.math.se/wikis/samverkan/linalg-LIU/index.php/Tips_och_l%C3%B6sning_till_%C3%B6vning_3.18a