Processing Math: Done
To print higher-resolution math symbols, click the
Hi-Res Fonts for Printing button on the jsMath control panel.
No jsMath TeX fonts found -- using image fonts instead.
These may be slow and might not print well.
Use the jsMath control panel to get additional information.
jsMath Control PanelHide this Message

jsMath

Tips och lösning till övning 3.5

SamverkanLinalgLIU

Hoppa till: navigering, sök

Tips 1

Rita en figur som beskriver projektionen av på samt på .

Tips 2

Använd projektionsformeln i de två fallen.

Tips 3

Det blir enklare att beräkna absolutbeloppen om man behåller faktorn framför vektorn.

Lösning

1. Vektorn är :s ortogonala projektion på och beräknas enligt

=2=1221112−36122122=11+22+2221+(−3)2+62122=98122

samt =98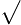1+22+22=38 .

2. Vidare är

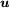=2=8492−36

amt =849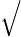22+(−3)2+62=78 .

Den här artikeln är hämtad från http://wiki.math.se/wikis/samverkan/linalg-LIU/index.php/Tips_och_l%C3%B6sning_till_%C3%B6vning_3.5