Processing Math: Done
Tips och lösning till övning 3.7
SamverkanLinalgLIU
Tips 1
Hej 1
Tips 2
Hej 2
Tips 3
Hej 3
Lösning
Eftersom  +3
+3
 −
−
 +3
+3 )
) (2
(2 −
− )=2
)=2

 2+5
2+5

 +
+

 2
2
På samma sätt följer att
 +7
+7 )
) (2
(2 +
+ )=2
)=2

 2+14
2+14

 +7
+7

 2
2
Vi får då följande ekvationssystem
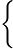 2
2

 2+5
2+5

 +
+

 22
22

 2+14
2+14

 +7
+7

 2==00
2==00

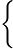


 2
2

 2==−
2==−

 −4
−4



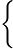





 ==
== −
−

 2
2 −
−


Vi ser här att 


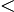 0
0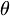


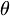 =
=








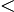 0
0

 2
2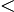
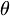
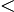 3
3
 2
2
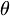 =
= 







 =
=

 2
2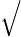 (
(

 )2=
)2=

 2(−
2(−

 )=−21
)=−21
Detta ger att 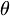 =32
=32
