Processing Math: Done
Tips och lösning till övning 3.9c
SamverkanLinalgLIU
Tips 1
Beräkna 
 1+
1+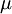
 3
3
Tips 2
Resultatet blir 
 1+
1+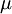
 3=
3=


 41−5
41−5

 +
+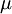


 −9−7 −3
−9−7 −3

 =
=

 4
4 −9
−9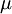
 −7
−7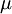 −5
−5 −3
−3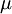



Tips 3
Sätt nu in koordinaterna för linjärkombinationen i vänsterledet i planets ekvation och kontrollera att resultatet blir noll (= högerledet)
Lösning
Vektorn 
 1+
1+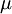
 3
3

 1+
1+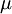
 3=
3=


 41−5
41−5

 +
+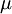


 −9−7 −3
−9−7 −3

 =
=

 4
4 −9
−9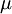
 −7
−7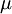 −5
−5 −3
−3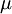



Vi sätter in koordinaterna i planets ekvation och får
 −9
−9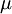 )−3(
)−3( −7
−7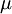 )+(−5
)+(−5 −3
−3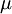 )=0
)=0
dvs 
 1+
1+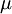
 3
3 U
U
